题目内容
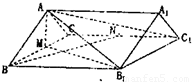
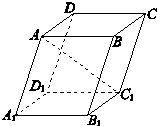如图，已知四棱柱ABCD-A1B1C1D1中，底面ABCD是边长为3的正方形，侧棱AA1长为4，且AA1与A1B1，A1D1的夹角都是60°，则AC1的长等于（ ）分析：直接根据向量的加法把所求问题分解，再平方计算出模长的平方，进而求出结论．
解答：解：因为
=
+
+
；
∴（
）2=（
+
+
）2
=（
）2+（
）2+（
）2+2
•
+2
•
+2
•
=42+32+32+2×4×3cos120°+2×4×3cos120°+2×3×3cos90°
=10．
∴AC1=
故选C．
解：因为 | AC1 |
| AA1 |
| A1B1 |
| B1C1 |
∴（
| AC1 |
| AA1 |
| A1B1 |
| B1C1 |
=（
| AA1 |
| A1B1 |
| B1C1 |
| AA1 |
| A1B1 |
| AA1 |
| B1C1 |
| A1B1 |
| B1C1 |
=42+32+32+2×4×3cos120°+2×4×3cos120°+2×3×3cos90°
=10．
∴AC1=
| 10 |
故选C．
点评：本题主要考查棱柱的结构特征以及两点间的距离计算．注意在利用两直线的夹角求向量夹角时，注意方向性，避免出错．
练习册系列答案
相关题目
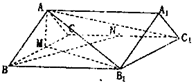如图，已知直棱柱ABC-A1B1C1中，AB=AC=5，BC=BB1=8，M，N分别为棱BC，CC1的中点．
（2007•无锡二模）如图，已知四棱柱ABCD-A1B1C1D1的底面ABCD为直角梯形，AB∥CD，AB⊥AD，AB=AD=A1B=2CD，侧面A1ADD1为正方形．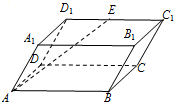
如图，已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形，AB=4，AA1=3，∠BAA1=60°，E为棱C1D1的中点，则
