题目内容
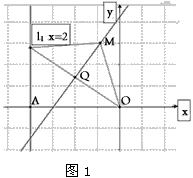
在平面直角坐标系xOy中,直线l:x=-2交x轴于点A,设P是l上一点,M是线段OP的垂直平分线上一点,且满足∠MPO=∠AOP。
(1)当点P在l上运动时,求点M的轨迹E的方程;
(2)已知T(1,-1),设H是E上动点,求|HO|+|HT|的最小值,并给出此时点H的坐标;
(3)过点T(1,-1)且不平行于y轴的直线l1与轨迹E有且只有两个不同的交点,求直线l1的斜率k的取值范围。
(1)当点P在l上运动时,求点M的轨迹E的方程;
(2)已知T(1,-1),设H是E上动点,求|HO|+|HT|的最小值,并给出此时点H的坐标;
(3)过点T(1,-1)且不平行于y轴的直线l1与轨迹E有且只有两个不同的交点,求直线l1的斜率k的取值范围。
|
解:(1)如图,设MQ为线段OP的垂直平分线,交OP于点Q, |
  |
(2)由(1)知,轨迹E的方程由E1和E2两部分组成 当 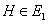 时,过T做垂直于L的直线,垂足为T′,交E1于点 时,过T做垂直于L的直线,垂足为T′,交E1于点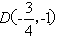 再过H做垂直于L的直线,交l于H ∴ 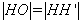 ∴ 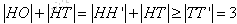 (该等号仅当H′与T′重合(或H与D重合)时取得) (该等号仅当H′与T′重合(或H与D重合)时取得)当 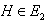 时,则 时,则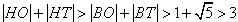 综合可得  的最小值为3,此时点H 的最小值为3,此时点H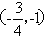 ; ; |
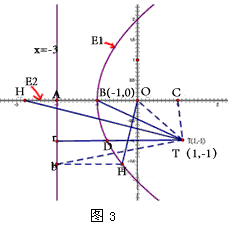 |
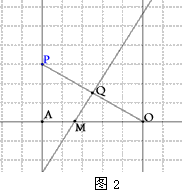
| (3)由图3可知,直线l1的斜率k不可能为0 设 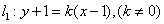 ∴ 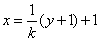 ,代入E1的方程得 ,代入E1的方程得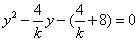 ∴ 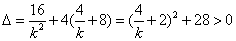 ∴l1与E中的E1有且仅有两个不同的交点 又由E2和l1的方程可知,若l1与E2有交点 则此交点的坐标为 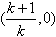 ,且 ,且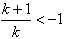 ,即当 ,即当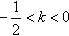 时l1与E2有唯一交点 时l1与E2有唯一交点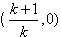 从上可知l1与E有三个不同的交点 ∴直线l1斜率k的取值范围是 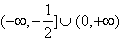 。 。 |

练习册系列答案
相关题目
在平面直角坐标系xOy中,双曲线中心在原点,焦点在y轴上,一条渐近线方程为x-2y=0,则它的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |


 ,即
,即



 即
即 得
得
 ;
; 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.