题目内容
已知函数f(x)=ax2+lnx(a∈R),
(Ⅰ)当a=2时,求f(x)在区间[e,e2]上的最大值和最小值;
(Ⅱ)如果函数g(x),f1(x),f2(x)在公共定义域D上,满足f1(x)<g(x)<f2(x),那么就称g(x)为f1(x),f2(x)的“伴随函数”。
已知函数f1(x)=(a-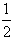 )x2+2ax+(1-a2)lnx,f2(x)=
)x2+2ax+(1-a2)lnx,f2(x)=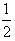 x2+2ax,若在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“伴随函数”,求a的取值范围。
x2+2ax,若在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“伴随函数”,求a的取值范围。
(Ⅰ)当a=2时,求f(x)在区间[e,e2]上的最大值和最小值;
(Ⅱ)如果函数g(x),f1(x),f2(x)在公共定义域D上,满足f1(x)<g(x)<f2(x),那么就称g(x)为f1(x),f2(x)的“伴随函数”。
已知函数f1(x)=(a-
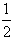 )x2+2ax+(1-a2)lnx,f2(x)=
)x2+2ax+(1-a2)lnx,f2(x)=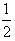 x2+2ax,若在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“伴随函数”,求a的取值范围。
x2+2ax,若在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“伴随函数”,求a的取值范围。 解:(Ⅰ)当a=2时,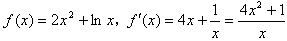 ;
;
对于 ,
,
∴f(x)在区间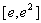 上为增函数,
上为增函数,
∴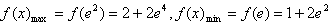 。
。
(Ⅱ)在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“伴随函数”,
则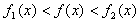 ,
,
令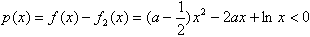 对x∈(1,+∞)恒成立,
对x∈(1,+∞)恒成立,
且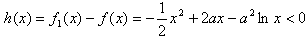 对x∈(1,+∞)恒成立,
对x∈(1,+∞)恒成立,
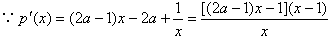 ,(*)
,(*)
①若 ,
,
当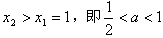 时,
时,
在 ,
,
此时p(x)在区间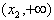 上是增函数,并且在该区间上有
上是增函数,并且在该区间上有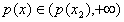 ,不合题意;
,不合题意;
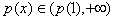 ,也不合题意;
,也不合题意;
②若 ,
,
此时在区间(1,+∞)上恒有p′(x)<0,
从而p(x)在区间(1,+∞)上是减函数;
要使p(x)<0在此区间上恒成立,只需满足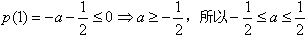 ;
;
又因为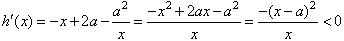 ,
,
h(x)在(1,+∞)上是减函数;
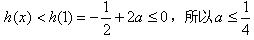 ,
,
综合可知a的取值范围是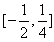 。
。
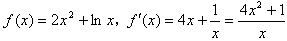 ;
;对于
 ,
,∴f(x)在区间
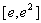 上为增函数,
上为增函数,∴
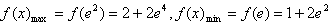 。
。(Ⅱ)在区间(1,+∞)上,函数f(x)是f1(x),f2(x)的“伴随函数”,
则
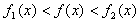 ,
,令
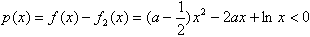 对x∈(1,+∞)恒成立,
对x∈(1,+∞)恒成立,且
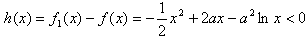 对x∈(1,+∞)恒成立,
对x∈(1,+∞)恒成立,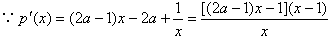 ,(*)
,(*)①若
 ,
,当
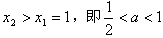 时,
时,在
 ,
,此时p(x)在区间
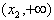 上是增函数,并且在该区间上有
上是增函数,并且在该区间上有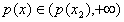 ,不合题意;
,不合题意;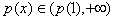 ,也不合题意;
,也不合题意;②若
 ,
,此时在区间(1,+∞)上恒有p′(x)<0,
从而p(x)在区间(1,+∞)上是减函数;
要使p(x)<0在此区间上恒成立,只需满足
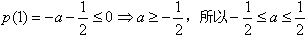 ;
;又因为
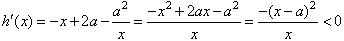 ,
,h(x)在(1,+∞)上是减函数;
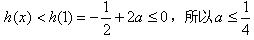 ,
,综合可知a的取值范围是
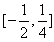 。
。 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目