题目内容
如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
(1)请画出表中数据的散点图;
(2)请求出y关于x的线性回归方程
=a+bx;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
注:线性回归方程系数公式
b=
=
,a=
-b
.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)请求出y关于x的线性回归方程
 |
| y |
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
注:线性回归方程系数公式
b=
| |||||||
|
| |||||||
|
. |
| y |
. |
| x |
分析:(1)利用表中数据描点,画图;
(2)根据所给的这组数据求出利用最小二乘法所需要的几个数据,代入求系数b的公式,求得结果,再把样本中心点代入,求出a的值,得到线性回归方程.
(3)根据上一问所求的线性回归方程,把x=100代入线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低标准煤的数量
(2)根据所给的这组数据求出利用最小二乘法所需要的几个数据,代入求系数b的公式,求得结果,再把样本中心点代入,求出a的值,得到线性回归方程.
(3)根据上一问所求的线性回归方程,把x=100代入线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低标准煤的数量
解答:(1)画出散点图.

解:(2)由对照数据,计算得
xi2=86,
=
=4.5,
=
=3.5,
xiyi=66.5,4
•
=63,4
2=81,
∴b=
=0.7,a=3.5-0.7×4.5=0.35,
∴所求线性回归方程为
=0.7x+0.35
(3)由(2)求出的线性回归方程,
预测生产100吨甲产品的生产能耗比技改前降低标准煤数量为:
90-(0.7×100+0.35)=19.65(吨标准煤吨).

解:(2)由对照数据,计算得
| 4 |
 |
| i=1 |
. |
| x |
| 3+4+5+6 |
| 4 |
. |
| y |
| 2.5+3+4+4.5 |
| 4 |
| 4 |
 |
| i=1 |
. |
| x |
. |
| y |
. |
| x |
∴b=
| 66.5-63 |
| 86-81 |
∴所求线性回归方程为
 |
| y |
(3)由(2)求出的线性回归方程,
预测生产100吨甲产品的生产能耗比技改前降低标准煤数量为:
90-(0.7×100+0.35)=19.65(吨标准煤吨).
点评:本题考查线性回归方程的求法与应用,本题是考查此类问题的典型题目,要注意掌握此类题目的解法.

练习册系列答案
相关题目
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产耗y(吨标准煤)的几对照数据
|
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y=![]() ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
(文)已知某几何体的俯视图是如图8所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.
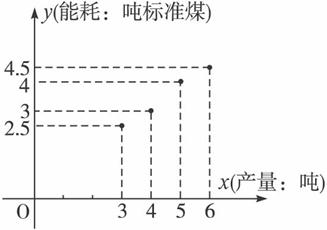
图8
(1)求该几何体的体积V;
(2)求该几何体的侧面积S.