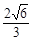题目内容

设F₁，F₂分别是椭圆 $数学公式$ 的左、右焦点，过F₁的直线l与E相交于A，B两点，且|AF₂|，|AB|，|BF₂|成等差数列，则|AB|的长为________．

$\text{[math]}$
分析：因为|AF₂|，|AB|，|BF₂|成等差数列，可得|AF₂|+|BF₂|=2|AB|，又|AF₂|+|A B|+|BF₂|=4，求出|AB|的长．
解答：∵|AF₂|，|AB|，|BF₂|成等差数列
∴|AF₂|+|BF₂|=2|AB|，
又椭圆 $\text{[math]}$ 中a=1
∴|AF₂|+|AB|+|BF₂|=4，∴3|AB|=4，
∴|AB|= $\text{[math]}$
故答案为： $\text{[math]}$
点评：本题考查椭圆的定义及其应用，把等差数列作为载体进行出题，考查圆锥曲线，是一种创新，属于基础题．

练习册系列答案

创新学习课课通系列答案

钟书金牌金牌一课一练系列答案

上海特训系列答案

互动英语系列答案

天天向上课时练系列答案

钟书金牌新学案作业本系列答案

新同步课课精练系列答案

导学先锋系列答案

零负担试卷系列答案

名牌学校分层周周测系列答案

相关题目

=1(a＞b＞0)短轴长为2，P（x₀，y₀）（x₀≠±a）是椭圆上一点，A，B分别是椭圆的左、右顶点，直线PA，PB的斜率之积为-

．
（1）求椭圆的方程；
（2）当∠F₁PF₂为钝角时，求P点横坐标的取值范围；
（3）设F₁，F₂分别是椭圆的左右焦点，M、N是椭圆右准线l上的两个点，若

=0，求MN的最小值．

（09年丰台区二模）（14分）

设F₁、F₂分别是椭圆的左、右焦点。

（I）若M是该椭圆上的一个动点，求的最大值和最小值；

（II）设过定点（0，2）的直线l与椭圆交于不同两点A、B，且∠AOB为钝角（其中O为坐标原点），求直线l的斜率k的取值范围。

设F₁、F₂分别是椭圆的左、右焦点，P为椭圆上一点，M是F₁P的中点，|OM|＝3，则P点到椭圆左焦点距离为 .

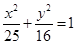设F₁、F₂分别是椭圆的左、右焦点，P为椭圆上任一点，点M的坐标为(6,4)，则|PM|＋|PF₁|的最大值为_______

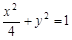设F₁，F₂分别是椭圆的左、右焦点，P是第一象限内该椭圆上的一点，且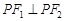，求点P的横坐标为（）

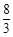A．1 B． C． D．