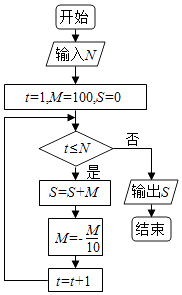
题目内容
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知sinA+ ![]() cosA=0,a=2
cosA=0,a=2 ![]() ,b=2.
,b=2.
(Ⅰ)求c;
(Ⅱ)设D为BC边上一点,且AD⊥AC,求△ABD的面积.
【答案】解:(Ⅰ)∵sinA+ ![]() cosA=0,
cosA=0,
∴tanA= ![]() ,
,
∵0<A<π,
∴A= ![]() ,
,
由余弦定理可得a2=b2+c2﹣2bccosA,
即28=4+c2﹣2×2c×(﹣ ![]() ),
),
即c2+2c﹣24=0,
解得c=﹣6(舍去)或c=4,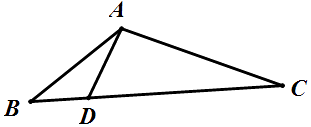
(Ⅱ)∵c2=b2+a2﹣2abcosC,
∴16=28+4﹣2×2 ![]() ×2×cosC,
×2×cosC,
∴cosC= ![]() ,
,
∴sinC= ![]() ,
,
∴tanC= ![]()
在Rt△ACD中,tanC= ![]() ,
,
∴AD= ![]() ,
,
∴S△ACD= ![]() ACAD=
ACAD= ![]() ×2×
×2× ![]() =
= ![]() ,
,
∵S△ABC= ![]() ABACsin∠BAD=
ABACsin∠BAD= ![]() ×4×2×
×4×2× ![]() =2
=2 ![]() ,
,
∴S△ABD=S△ABC﹣S△ADC=2 ![]() ﹣
﹣ ![]() =
= ![]()
【解析】(Ⅰ)先根据同角的三角函数的关系求出A,再根据余弦定理即可求出,
(Ⅱ)先根据夹角求出cosC,求出AD的长,再求出△ABC和△ADC的面积,即可求出△ABD的面积.
【考点精析】解答此题的关键在于理解同角三角函数基本关系的运用的相关知识,掌握同角三角函数的基本关系:![]()
![]() ;
;![]()
![]() ;(3) 倒数关系:
;(3) 倒数关系:![]() .
.

练习册系列答案
相关题目