题目内容
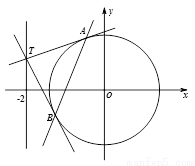
(本题满分15分) 设点 为圆
为圆 上的动点,过点
上的动点,过点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 .动点
.动点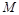 满足
满足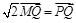 (其中
(其中 ,
, 不重合).
不重合).
(Ⅰ)求点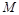 的轨迹
的轨迹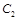 的方程;
的方程;
(Ⅱ)过直线 上的动点
上的动点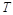 作圆
作圆 的两条切线,设切点分别为
的两条切线,设切点分别为 .若直线
.若直线 与(Ⅰ)中的曲线
与(Ⅰ)中的曲线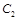 交于
交于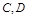 两点,求
两点,求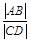 的取值范围.
的取值范围.
【答案】
(Ⅰ)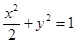 .(Ⅱ)
.(Ⅱ)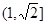
【解析】解:(Ⅰ)设点M(x,y),由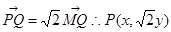 ,由于点P在
,由于点P在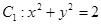 上,则
上,则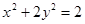 ,
,
即M的轨迹方程为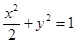 .
……4′
.
……4′
(Ⅱ)设点T(-2,t),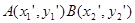 ,则AT,BT的方程为:
,则AT,BT的方程为: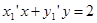 ,
,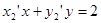 ,
,
又点T(-2,t) 在AT、BT上,则有:
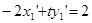 ①,
①,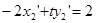 ②,由①、②知AB的方程为:
②,由①、②知AB的方程为: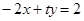 . ……3′
. ……3′
设点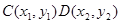 ,则圆心O到AB的距离
,则圆心O到AB的距离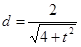 ,
,
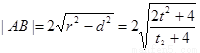 ;又由
;又由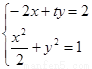 ,得
,得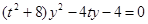 ,于是
,于是
 ,,于是
,,于是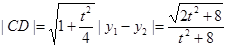
于是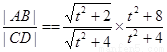 , ……3′
, ……3′
设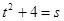 ,则
,则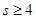 ,于是
,于是 ,设
,设 ,于是
,于是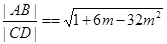 ,设
,设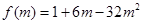 ,
,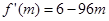 ,令
,令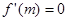 ,得m=1/4.
,得m=1/4.
得f(m)在(0,1/4】上单调递增,故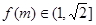 .
.
即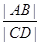 的范围为
的范围为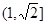 ……5′
……5′
思路分析:第一问中利用向量的关系式消元法得到轨迹方程。设点M(x,y),由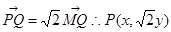 ,由于点P在
,由于点P在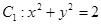 上,则
上,则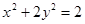 ,
,
第二问,设点T(-2,t),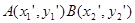 ,则AT,BT的方程为:
,则AT,BT的方程为: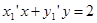 ,
,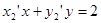 ,
,
又点T(-2,t) 在AT、BT上,则有:
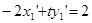 ①,
①,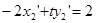 ②,由①、②知AB的方程为:
②,由①、②知AB的方程为: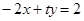 . ……3′
. ……3′
设点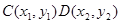 ,则圆心O到AB的距离
,则圆心O到AB的距离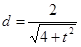
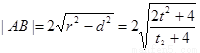 ;又由
;又由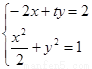 ,得
,得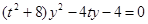 ,于是
,于是
 ,,于是
,,于是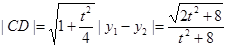
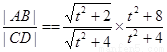 构造函数求解得到。
构造函数求解得到。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
. 在
在 上单调递增,在
上单调递增,在 上单调递减,求实数
上单调递减,求实数 的最大值;
的最大值; 对任意的
对任意的 ,
, 都成立,求实数
都成立,求实数 的取值范围.
的取值范围. 为自然对数的底数.
为自然对数的底数. 与曲线
与曲线 相切
相切 在
在 上恰有两个不等的实数根
上恰有两个不等的实数根 ,求
,求 的大小
的大小 :
: (
( ),焦点为
),焦点为 ,直线
,直线 交抛物线
交抛物线 、
、 两点,
两点, 是线段
是线段 的中点,
的中点, 轴的垂线交抛物线
轴的垂线交抛物线 ,
, 到焦点
到焦点 ,求此时
,求此时 的值;
的值; 是以
是以

 的单调区间;
的单调区间; ,若
,若 在
在 上不单调且仅在
上不单调且仅在 处取得最大值,求
处取得最大值,求 的取值范围.
的取值范围.