题目内容
若函数g(x)=x3-ax2+1在区间[1,2]上是单调递减函数,则实数a的取值范围是______.
由g(x)=x3-ax2+1,所以g′(x)=3x2-2ax,
因为 g(x)=x3-ax2+1在区间[1,2]上是单调递减函数,
所以以g′(x)=3x2-2ax≤0在x∈[1,2]上恒成立.
即2ax≥3x2,a≥
x在x∈[1,2]上恒成立.
因为函数y=
x在x∈[1,2]上为增函数,所以ymax=
×2=3.
所以a≥3.
故答案为a≥3.
因为 g(x)=x3-ax2+1在区间[1,2]上是单调递减函数,
所以以g′(x)=3x2-2ax≤0在x∈[1,2]上恒成立.
即2ax≥3x2,a≥
| 3 |
| 2 |
因为函数y=
| 3 |
| 2 |
| 3 |
| 2 |
所以a≥3.
故答案为a≥3.

练习册系列答案
相关题目
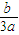 ,f(-
,f(-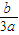 ))对称:
))对称: x3-
x3- x2-
x2-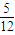 ,则,g(
,则,g(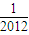 )+g(
)+g(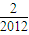 )+g(
)+g(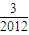 )+…+g(
)+…+g(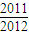 )=-105.5.
)=-105.5. ,f(-
,f(- ))对称:
))对称: x3-
x3- x2-
x2- ,则,g(
,则,g( )+g(
)+g( )+g(
)+g(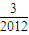 )+…+g(
)+…+g( )=-105.5.
)=-105.5. x3-
x3- x2+3x-
x2+3x-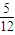 +
+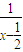 ,则g(
,则g(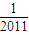 )+g(
)+g(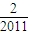 )+g(
)+g(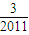 )+g(
)+g(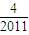 )+…+g(
)+…+g(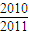 )= .
)= .