题目内容
已知x,y≠kπ+
(k∈Z),sinx是sinθ,cosθ的等差中项,siny是sinθ,cosθ的等比中项.
求证:(1)cos2x=
cos2y;(2)
=
.
| π |
| 2 |
求证:(1)cos2x=
| 1 |
| 2 |
| 2(1-tan2x) |
| 1+tan2x |
| 1-tan2y |
| 1+tan2y |
证明:(1)∵sinθ与cosθ的等差中项是sinx,等比中项是siny,
∴sinθ+cosθ=2sinx①,sinθcosθ=sin2y②,
①2-②×2,可得(sinθ+cosθ)2-2sinθcosθ=4sin2x-2sin2y,即4sin2x-2sin2y=1.
∴4×
-2×
=1,即2-2cos2x-(1-cos2y)=1.
故证得cos2x=
cos2y;
(2)要证
=
,只需证
=
,
即证
=
,即证cos2x-sin2x=
(cos2y-sin2y),只需证cos2x=
cos2y.
由(1)的结论,cos2x=
cos2y显然成立.
所以
=
.
∴sinθ+cosθ=2sinx①,sinθcosθ=sin2y②,
①2-②×2,可得(sinθ+cosθ)2-2sinθcosθ=4sin2x-2sin2y,即4sin2x-2sin2y=1.
∴4×
| 1-cos2x |
| 2 |
| 1-cos2y |
| 2 |
故证得cos2x=
| 1 |
| 2 |
(2)要证
| 2(1-tan2x) |
| 1+tan2x |
| 1-tan2y |
| 1+tan2y |
1-
| ||
1+
|
1-
| ||
2(1+
|
即证
| cos2x-sin2x |
| cos2x+sin2x |
| cos2y-sin2y |
| 2(cos2y+sin2y) |
| 1 |
| 2 |
| 1 |
| 2 |
由(1)的结论,cos2x=
| 1 |
| 2 |
所以
| 2(1-tan2x) |
| 1+tan2x |
| 1-tan2y |
| 1+tan2y |

练习册系列答案
相关题目
 (k∈Z),sinx是sinθ,cosθ的等差中项,siny是sinθ,cosθ的等比中项.
(k∈Z),sinx是sinθ,cosθ的等差中项,siny是sinθ,cosθ的等比中项. cos2y;(2)
cos2y;(2)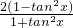 =
=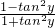 .
.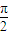 (k∈Z),sinx是sinθ,cosθ的等差中项,siny是sinθ,cosθ的等比中项.
(k∈Z),sinx是sinθ,cosθ的等差中项,siny是sinθ,cosθ的等比中项. cos2y;(2)
cos2y;(2)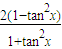 =
=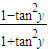 .
.