题目内容

若a＞0，a≠1，x＞y＞0（n∈N^+）则下列各式成立的有________．
①（log_ax）ⁿ=nlog_ax②（log_ax）ⁿ=log_axⁿ③ $数学公式$ ④ $数学公式$
⑤ $数学公式$ ⑥ $数学公式$ ⑦ $数学公式$ ⑧ $数学公式$

③⑧
分析：根据已知条件，结合对数的性质，逐个对式子进行判断证明，可得到答案，也可利用特值法，代入进行判断．
解答：由对数的运算性质：
nlog_ax=log_axⁿ≠（log_ax）ⁿ，故①②⑤⑥⑦错误；
∵ $\text{[math]}$ =x^-1∴ $\text{[math]}$ ，故③正确；
同理⑧正确；
由换底公式易得：④错误；
故答案为：③⑧
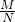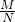点评：解决本题的关键是熟练掌握对数的运算性质：如果a＞0，且a≠1，M＞0，N＞0，那么：①log_a（M•N）=log_aM+log_aN；②log_a（ $\text{[math]}$ ）=log_aM-log_aN；③log_aMⁿ=n•log_aM（n∈R）；

练习册系列答案

一通百通考必赢系列答案

一线名师夺冠王检测卷系列答案

一线名师提优试卷系列答案

一路领先优选卷系列答案

一路领先口算题卡系列答案

一课3练课时导练系列答案

一飞冲天课时作业系列答案

一本到位系列答案

阳光试卷单元测试卷系列答案

阳光课堂星球地图出版社系列答案

相关题目

有下列命题：
①函数y=f （-x+2）与y=f （x-2）的图象关于y轴对称；
②若函数f（x）=e^x，则?x₁，x₂∈R，都有f(

；
③若函数f（x）=log_a|x|（a＞0，a≠1）在（0，+∞）上单调递增，则f（-2）＞f（a+1）；
④若函数f（x+2010）=x²-2x-1（x∈R），则函数f（x）的最小值为-2．
其中真命题的序号是

有下列命题：
①函数y=f （-x+2）与y=f （x-2）的图象关于y轴对称；
②若函数f（x）=e^x，则?x₁，x₂∈R，都有f(

；
③若函数f（x）=log_a|x|（a＞0，a≠1）在（0，+∞）上单调递增，则f（-2）＞f（a+1）；
④若函数f（x+2010）=x²-2x-1 （x∈R），则函数f（x）的最小值为-2．
其中真命题的序号是

若a＞0且a≠1，x∈R，y∈R且xy＞0，则下列各式中错误的是

①log_ax²＝2log_ax

②log_ax²＝2log_a|x|

③log_axy＝log_ax＋log_ay

④log_axy＝log_a|x|＋log_a|y

A．②④

B．①③

C．①④

D．②③

若a＞0，a≠1，x＞0，y＞0，x＞y，下列式子中正确的个数为

①log_ax＋log_ay＝log_a(x＋y)

②log_ax－log_ay＝log_a(x－y)

③log_a＝log_ax÷log_ay

④log_a(x·y)＝log_ax·log_ay

0

1

2

3

若a＞0，a≠1，x＞0，y＞0，x＞y，下列式子中正确的个数有

①log_ax·log_ay＝log_a(x＋y)；

②log_ax－log_ay＝log_a(x－y)；

③log_a＝log_ax÷log_ay；

④log_a(xy)＝log_ax·log_ay．

A．0

B．1

C．2

D．3