题目内容
 某货船在索马里海域航行中遭遇海盗袭击,发出呼救信号,我海军护航舰在A处获悉后,立即测出该船在方位角45°,距离10海里的C处,并测得该船正沿方位角105°的方向,以每小时10海里的速度向前行驶,我海军护航舰立即以每小时10
某货船在索马里海域航行中遭遇海盗袭击,发出呼救信号,我海军护航舰在A处获悉后,立即测出该船在方位角45°,距离10海里的C处,并测得该船正沿方位角105°的方向,以每小时10海里的速度向前行驶,我海军护航舰立即以每小时10| 3 |
分析:设所需时间为th,可得AB=10
t且CB=10t,△ABC中由余弦定理建立关于t的方程,解出t=1,从而得到AB=10
、BC=10.然后由正弦定理解出∠CAB=30°,即可得到护航舰航行的方位角.
| 3 |
| 3 |
解答:解:如图所示,设所需时间为t小时,AB=10
t,CB=10t
在△ABC中,由余弦定理AB2=BC2+AC2-2BC•ACcos∠BAC,
得300t2=100t2+100-2•10t•10cos120°
解之得t=1或t=-
,
所以护航舰需要1小时靠近货船.--------------(6分).
此时AB=10
,BC=10,
在△ABC中,由正弦定理得
=
,
即
=
,解得sin∠CAB=
∵∠CAB∈(0,
),∴∠CAB=30°,
由此可得:护航舰航行的方位角为45°+30°=75°.
∴护航舰的舰向为北偏东75°,靠近货船所需的时间为1小时---------(12分)
| 3 |
在△ABC中,由余弦定理AB2=BC2+AC2-2BC•ACcos∠BAC,
得300t2=100t2+100-2•10t•10cos120°
解之得t=1或t=-
| 1 |
| 2 |
所以护航舰需要1小时靠近货船.--------------(6分).
此时AB=10
| 3 |
在△ABC中,由正弦定理得
| BC |
| sin∠CAB |
| AB |
| sin120° |
即
| 10 |
| sin∠CAB |
10
| ||||
|
| 1 |
| 2 |
∵∠CAB∈(0,
| π |
| 2 |
由此可得:护航舰航行的方位角为45°+30°=75°.
∴护航舰的舰向为北偏东75°,靠近货船所需的时间为1小时---------(12分)
点评:本题给出实际应用问题,求护航舰的航向和所需时间,着重考查了利用正余弦定理解三角形及其应用等知识,属于中档题.

练习册系列答案
相关题目
 某种日用品上市以后供不应求,为满足更多的消费者,某商场在销售的过程中要求购买这种产品的顾客必须参加如下活动:摇动如图所示的游戏转盘(上面扇形的圆心角都相等),按照指针所指区域的数字购买商品的件数,每人只能参加一次这个活动.
某种日用品上市以后供不应求,为满足更多的消费者,某商场在销售的过程中要求购买这种产品的顾客必须参加如下活动:摇动如图所示的游戏转盘(上面扇形的圆心角都相等),按照指针所指区域的数字购买商品的件数,每人只能参加一次这个活动.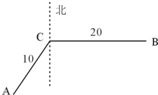 如图,中国在索马里海域值勤的A船接到B处一货船遇险求救信号,A船立即前往营救,同时把消息告知在A船东偏北60°相距10n,mil的C船,此时C船在B的正西方,相距20n,mil处.
如图,中国在索马里海域值勤的A船接到B处一货船遇险求救信号,A船立即前往营救,同时把消息告知在A船东偏北60°相距10n,mil的C船,此时C船在B的正西方,相距20n,mil处. (2011•滨州一模)我市某商场在春节促销活动中,对2011年2月2日10时至15时的销售额进行统计,其频率分布直方图如图所示,已知10时至11时销售额为3万元,则11时至13时的销售额为
(2011•滨州一模)我市某商场在春节促销活动中,对2011年2月2日10时至15时的销售额进行统计,其频率分布直方图如图所示,已知10时至11时销售额为3万元,则11时至13时的销售额为