题目内容
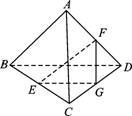
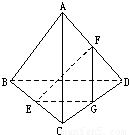
A是△BCD平面外的一点，E、F分别是BC、AD的中点，
（1）求证：直线EF与BD是异面直线；
（2）若AC⊥BD，AC=BD，求EF与BD所成的角．
（1）求证：直线EF与BD是异面直线；
（2）若AC⊥BD，AC=BD，求EF与BD所成的角．
（1）证明：用反证法．设EF与BD不是异面直线，
则EF与BD共面，从而DF与BE共面，即AD与BC共面，
所以A、B、C、D在同一平面内，
这与A是△BCD平面外的一点相矛盾．
故直线EF与BD是异面直线．
（2）取CD的中点G，连接EG、FG，
则EG∥BD，
所以相交直线EF与EG所成的锐角或直角即为异面直线EF与BD所成的角．
在Rt△EGF中，求得∠FEG=45°，
即异面直线EF与BD所成的角为45°．
则EF与BD共面，从而DF与BE共面，即AD与BC共面，
所以A、B、C、D在同一平面内，
这与A是△BCD平面外的一点相矛盾．
故直线EF与BD是异面直线．
（2）取CD的中点G，连接EG、FG，
则EG∥BD，
所以相交直线EF与EG所成的锐角或直角即为异面直线EF与BD所成的角．
在Rt△EGF中，求得∠FEG=45°，
即异面直线EF与BD所成的角为45°．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
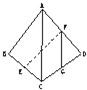11、A是△BCD平面外的一点，E、F分别是BC、AD的中点，
A是△BCD平面外的一点，E、F分别是BC、AD的中点，若AC⊥BD，AC=BD，求EF与BD所成的角．
