题目内容
已知数列{an}的前n项和为Sn,且a1=4,Sn=nan+2-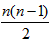 (n≥2,n∈N*)
(n≥2,n∈N*)
(1)求数列{an}的通项公式;
(2)设数列{bn}满足:b1=4,且bn+1=bn2-(n-1)bn-2(n∈N*),求证:bn>an(n≥2,n∈N*);
(3)求证: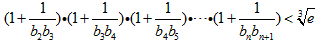 (n≥2,n∈N*)
(n≥2,n∈N*)
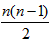 (n≥2,n∈N*)
(n≥2,n∈N*)(1)求数列{an}的通项公式;
(2)设数列{bn}满足:b1=4,且bn+1=bn2-(n-1)bn-2(n∈N*),求证:bn>an(n≥2,n∈N*);
(3)求证:
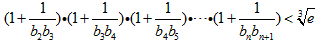 (n≥2,n∈N*)
(n≥2,n∈N*)解:(1)当n≥3时,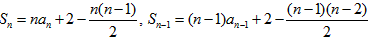
可得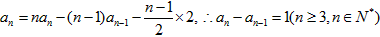
∵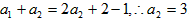 可得
可得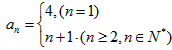
(2)1°当n=2时,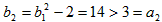 不等式成立;
不等式成立;
2°假设当n=k(k≥2,k∈N*)时,不等式成立,即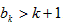 ,
,
那么,当n=k+1时,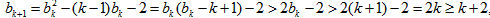
所以当n=k+1时,不等式也成立;
根据(1°),(2°)可知,当n≥2,n∈N*时,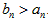
(3)设f(x)=ln(1+x)-x,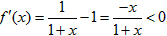
∴f(x)在(0,+∞)上单调递减,∴f(x)<f(0),∴ln(1+x)<x
∵当n≥2,n∈N*时,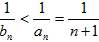
∴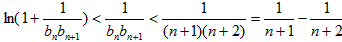
∴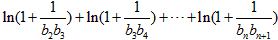
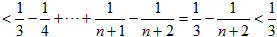
∴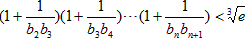 。
。
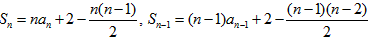
可得
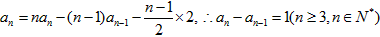
∵
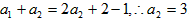 可得
可得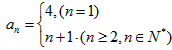
(2)1°当n=2时,
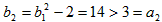 不等式成立;
不等式成立;2°假设当n=k(k≥2,k∈N*)时,不等式成立,即
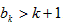 ,
,那么,当n=k+1时,
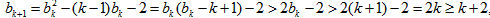
所以当n=k+1时,不等式也成立;
根据(1°),(2°)可知,当n≥2,n∈N*时,
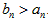
(3)设f(x)=ln(1+x)-x,
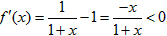
∴f(x)在(0,+∞)上单调递减,∴f(x)<f(0),∴ln(1+x)<x
∵当n≥2,n∈N*时,
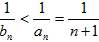
∴
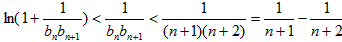
∴
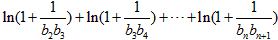
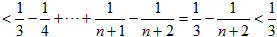
∴
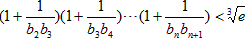 。
。
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |