题目内容
已知过点P的直线l绕点P按逆时针方向旋转α角(0<α<
),得直线为x-y-2=0,若继续按逆时针方向旋转
-α角,得直线2x+y-1=0,求直线l的方程.
| π |
| 2 |
| π |
| 2 |
分析:联立两直线的方程求出p的坐标,根据题意判断出直线l与直线2x+y-1=0垂直,求出l的斜率,利用直线的点斜式写出直线的方程.
解答:解:由
得P(1,-1)
据题意,直线l与直线2x+y-1=0垂直,
故l斜率k=
∴直线l方程为 y+1=
(x-1),
即x-2y-3=0.
|
据题意,直线l与直线2x+y-1=0垂直,
故l斜率k=
| 1 |
| 2 |
∴直线l方程为 y+1=
| 1 |
| 2 |
即x-2y-3=0.
点评:本题考查两直线交点的求法、直线垂直斜率的关系及直线的点斜式形式,属于基础题.

练习册系列答案
相关题目
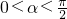 ),得直线为x-y-2=0,若继续按逆时针方向旋转
),得直线为x-y-2=0,若继续按逆时针方向旋转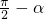 角,得直线2x+y-1=0,求直线l的方程.
角,得直线2x+y-1=0,求直线l的方程. ),得直线为x-y-2=0,若继续按逆时针方向旋转
),得直线为x-y-2=0,若继续按逆时针方向旋转 角,得直线2x+y-1=0,求直线l的方程.
角,得直线2x+y-1=0,求直线l的方程.