题目内容
19.函数y=|x-2|-|x+1|的取值范围为[-3,3].分析 化简函数,分别确定其范围,即可得出函数y=|x-2|-|x+1|的取值范围.
解答 解:当-1<x<2时,y=2-x-x-1=1-2x∈(-3,3);
当x≤-1时,y=2-x+(x+1)=3;
当x≥2时,y=x-2-(x+1)=-3,
所以y的取值范围是[-3,3].
故答案为:[-3,3].
点评 本题考查求函数y=|x-2|-|x+1|的取值范围,正确讨论是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.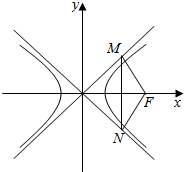 如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )
如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )
 如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )
如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )| A. | (1,$\sqrt{2}$) | B. | (1,2) | C. | ($\sqrt{2}$,+∞) | D. | (2,+∞) |
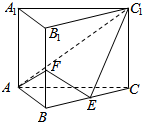 已知在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=2,E,F分别是BC,BB1的中点.
已知在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=2,E,F分别是BC,BB1的中点.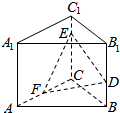 如图,已知正三棱柱ABC-A1B1C1中,AA1=4,AB=6,点D,E,F分别在棱BB1,CC1,AF上,且BD=C1E=$\frac{1}{2}$AF=1.
如图,已知正三棱柱ABC-A1B1C1中,AA1=4,AB=6,点D,E,F分别在棱BB1,CC1,AF上,且BD=C1E=$\frac{1}{2}$AF=1.