题目内容
已知函数f（x）=sin（ωx+φ），其中ω＞0，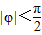
．（I）若
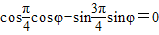，求φ的值；（Ⅱ）在（I）的条件下，若函数f（x）的图象的相邻两条对称轴之间的距离等于
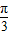，求当
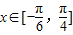时，函数f（x）的值域．
【答案】分析：（1）条件：“
”形式是两角和余弦函数，可转化成一个角的三角函数，从而解三角方程求出φ；
（2）如下图，相邻两条对称轴之间的距离等于半个周期，由此可求出ω，从而可求出f（x）的解析式，再结合下面图形中正弦函数的
单调性，求出函数f（x）的值域．
解答：
解：（I）由
得
即
又
（Ⅱ）由（I）得，
，依题意，结合图：
，
，又
，
故ω=3，∴
，
∵
，∴
，∴
，
函数f（x）的值域为
．
点评：三角函数的图象与性质是三角函数的重要内容，三角函数的单调性与对称性是函数的重要性质，合理使用函数的性质，正确理解它们的含义，是熟练利用这些基本性质解综合问题的前提．
”形式是两角和余弦函数，可转化成一个角的三角函数，从而解三角方程求出φ；（2）如下图，相邻两条对称轴之间的距离等于半个周期，由此可求出ω，从而可求出f（x）的解析式，再结合下面图形中正弦函数的
单调性，求出函数f（x）的值域．
解答：
解：（I）由得即
又（Ⅱ）由（I）得，
，依题意，结合图：，
，又，故ω=3，∴
，∵
，∴，∴，函数f（x）的值域为
．点评：三角函数的图象与性质是三角函数的重要内容，三角函数的单调性与对称性是函数的重要性质，合理使用函数的性质，正确理解它们的含义，是熟练利用这些基本性质解综合问题的前提．
练习册系列答案
相关题目
