题目内容

设函数f(x)=（x2+ax+a）e-x，其中x∈R，
(Ⅰ)确定a的值，使f(x)的极小值为0；
(Ⅱ)证明：当且仅当a=3时，f（x）的极大值为3。 

解：(Ⅰ)由于，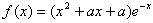
所以，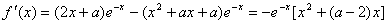
令f′(x)=0，解得：x=0或x=2-a，
①当a=2时，f′(x)≤0，此时无极值；
②当0＜2-a，即a＜2时，f′(x)和f(x)的变化如下表1，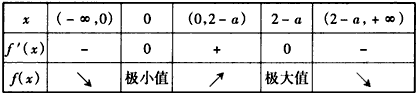

此时应有f(0)=0，所以，a=0＜2；
③当0＞2-a，即a＞2时，f′(x)和f(x)的变化如下表2，

此时应有f(2-a)=0，即，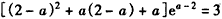
所以必有；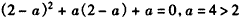
综上所述，当a=0或a=4时，f(x)的极小值为0。
(Ⅱ)若a＜2，则由表1知，应有f(2-a)=3，
即，
∴，
设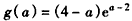，则，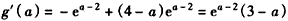
由a＜2，故g′(x)＞0，
于是当a＜2时，g(a)＜g(2)=2＜3，即不可能成立；
若a＞2，则由表2知，应有f(0)=3，即a=3；
综上所述，当且仅当a=3时极大值为3。

练习册系列答案
相关题目
设函数f（x）的定义域为D，若存在非零常数l，使得对于任意x⊆M（M⊆D）都有f（x+l）≥f（x），则称f（x）为M上的高调函数，l是一个高调值．
现给出下列命题：
①函数f（x）=(
1
2
)x为R上的高调函数；
②函数f（x）=sin2x为R上的高调函数
③若函数f（x）=x2+2x为（-∞，1]上的高调函数，则高调值l的取值范围是（-∞，-4]．
其中正确的命题个数是（　　）
A、0个B、1个C、2个D、3个
设二次函数f（x）=ax2+bx+c（a≠0）满足条件：①当x∈R时，f（x-4）=f（2-x），且x≤f(x)≤
12
(1+x2)；②f（x）在R上的最小值为0．
（1）求f（1）的值及f（x）的解析式；
（2）若g（x）=f（x）-k2x在[-1，1]上是单调函数，求k的取值范围；
（3）求最大值m（m＞1），使得存在t∈R，只要x∈[1，m]，就有f（x+t）≤x．
设函数f（x）的定义域为D，若存在非零实数h使得对于任意x∈M（M⊆D），有x+h⊆D，且f（x+h）≥f（x），则称f（x）为M上的“h阶高调函数”．给出如下结论：
①若函数f（x）在R上单调递增，则存在非零实数h使f（x）为R上的“h阶高调函数”；
②若函数f（x）为R上的“h阶高调函数”，则f（x）在R上单调递增；
③若函数f（x）=x2为区间[-1，+∞）上的“h阶高诬蔑财函数”，则h≥2；
④若函数f（x）在R上的奇函数，且x≥0时，f（x）=|x-1|-1，则f（x）只能是R上的“4阶高调函数”．
其中正确结论的序号为（　　）

设函数f（x）的定义域为D，若存在非零实数h使得对于任意x∈M（M⊆D），有x+h⊆D，且f（x+h）≥f（x），则称f（x）为M上的“h阶高调函数”．给出如下结论：
①若函数f（x）在R上单调递增，则存在非零实数h使f（x）为R上的“h阶高调函数”；
②若函数f（x）为R上的“h阶高调函数”，则f（x）在R上单调递增；
③若函数f（x）=x2为区间[-1，+∞）上的“h阶高诬蔑财函数”，则h≥2；
④若函数f（x）在R上的奇函数，且x≥0时，f（x）=|x-1|-1，则f（x）只能是R上的“4阶高调函数”．
其中正确结论的序号为


  1. A.
    ①③
  2. B.
    ①④
  3. C.
    ②③
  4. D.
    ②④
设二次函数f（x）=ax2+bx+c（a≠0）满足条件：①当x∈R时，f（x-4）=f（2-x），且x≤f(x)≤
1
2
(1+x2)；②f（x）在R上的最小值为0．
（1）求f（1）的值及f（x）的解析式；
（2）若g（x）=f（x）-k2x在[-1，1]上是单调函数，求k的取值范围；
（3）求最大值m（m＞1），使得存在t∈R，只要x∈[1，m]，就有f（x+t）≤x．