题目内容
设数列{an}满足an+1=an2-nan+1,n=1,2,3,…,
(Ⅰ)当a1=2时,求a2,a3,a4,并由此猜想出an的一个通项公式;
(Ⅱ)当a1≥3时,证明对所有的n≥1,有
(ⅰ)an≥n+2;
(ⅱ)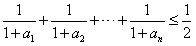 。
。
(Ⅰ)当a1=2时,求a2,a3,a4,并由此猜想出an的一个通项公式;
(Ⅱ)当a1≥3时,证明对所有的n≥1,有
(ⅰ)an≥n+2;
(ⅱ)
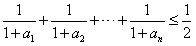 。
。解:(Ⅰ)由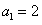 ,得
,得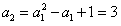 ;
;
由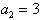 ,得
,得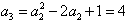 ;
;
由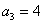 ,得
,得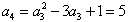 ;
;
由此猜想an的一个通项公式: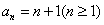 。
。
(Ⅱ)(ⅰ)用数学归纳法证明:
①当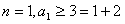 ,不等式成立;
,不等式成立;
②假设当n=k时不等式成立,即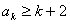 ,
,
那么,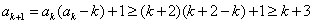 ,
,
也就是说,当n=k+1时,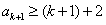 ,
,
根据①和②,对于所有n≥1,有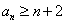 。
。
(ⅱ)由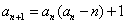 及(ⅰ),对k≥2,
及(ⅰ),对k≥2,
有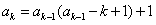
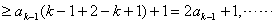 ,
,
∴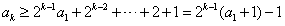 ,
,
于是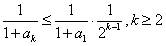 ,
,
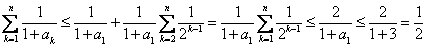 。
。
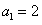 ,得
,得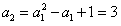 ;
;由
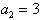 ,得
,得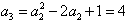 ;
;由
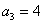 ,得
,得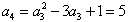 ;
;由此猜想an的一个通项公式:
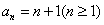 。
。(Ⅱ)(ⅰ)用数学归纳法证明:
①当
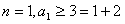 ,不等式成立;
,不等式成立;②假设当n=k时不等式成立,即
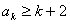 ,
,那么,
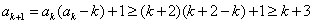 ,
,也就是说,当n=k+1时,
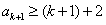 ,
,根据①和②,对于所有n≥1,有
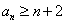 。
。(ⅱ)由
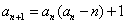 及(ⅰ),对k≥2,
及(ⅰ),对k≥2,有
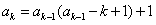
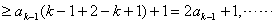 ,
,∴
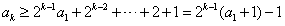 ,
,于是
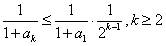 ,
,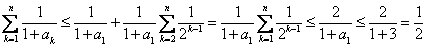 。
。
练习册系列答案
相关题目
设数列{an}满足a1=1,a2+a4=6,且对任意n∈N*,函数f(x)=(an-an+1+an+2)x+an+1?cosx-an+2sinx满足f′(
)=0若cn=an+
,则数列{cn}的前n项和Sn为( )
| π |
| 2 |
| 1 |
| 2an |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|