题目内容
函数f(x)=xecosx(x∈[-π,π])的图象大致是( )A.
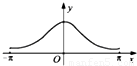
B.
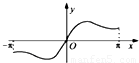
C.
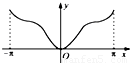
D.
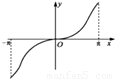
【答案】分析:通过y=ecosx与y=x的奇偶性以及函数在y=x的单调性,即可判断选项.
解答:解:因为y=ecosx,f(-x)=ecos(-x)=ecosx=f(x),所以y=ecosx是偶函数,y=x是奇函数,
函数f(x)=xecosx(x∈[-π,π])是奇函数,
所以A、C不正确,
f(π)=πecosπ=π,所以f(x)=xecosx经过(π,π)点
故选D.
点评:本题考查函数的奇偶性与函数的单调性的综合应用,函数的图象的判断,考查分析问题解决问题的能力.
解答:解:因为y=ecosx,f(-x)=ecos(-x)=ecosx=f(x),所以y=ecosx是偶函数,y=x是奇函数,
函数f(x)=xecosx(x∈[-π,π])是奇函数,
所以A、C不正确,
f(π)=πecosπ=π,所以f(x)=xecosx经过(π,π)点
故选D.
点评:本题考查函数的奇偶性与函数的单调性的综合应用,函数的图象的判断,考查分析问题解决问题的能力.

练习册系列答案
相关题目
已知函数f(x)满足f(0)=1,f(x+1)=
+f(x) (x∈R),则数列{f(n)}的前20项和为( )
| 3 |
| 2 |
| A、305 | B、315 |
| C、325 | D、335 |