题目内容
函数y=2cos2x+4cosx-1(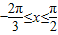 )的值域是 .
)的值域是 .
【答案】分析:可得y=(2cosx+1)2-4,令t=cosx,可得y=(2t+1)2-4,由关于t的二次函数区间的最值可得.
解答:解:由二倍角的余弦公式可得y=2(2cos2x-1)+4cosx-1
=4cos2x+4cosx-3=(2cosx+1)2-4,
∵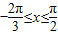 ,∴t=cosx∈[-1,1],
,∴t=cosx∈[-1,1],
故原函数可化为y=(2t+1)2-4,
函数为开口向上,对称轴为t=- 的抛物线一段,
的抛物线一段,
故函数在[-1,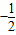 ]单调递减,在[
]单调递减,在[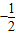 ,1]单调递增,
,1]单调递增,
故当t=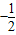 时,函数取最小值ymin=-4,
时,函数取最小值ymin=-4,
当t=1时,函数取最大值ymax=5
故函数的值域为[-4,5]
故答案为:[-4,5]
点评:本题考查二次函数在闭区间的最值,利用二倍角的余弦公式化为关于t的二次函数的区间最值是解决问题的关键,属中档题.
解答:解:由二倍角的余弦公式可得y=2(2cos2x-1)+4cosx-1
=4cos2x+4cosx-3=(2cosx+1)2-4,
∵
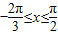 ,∴t=cosx∈[-1,1],
,∴t=cosx∈[-1,1],故原函数可化为y=(2t+1)2-4,
函数为开口向上,对称轴为t=-
 的抛物线一段,
的抛物线一段,故函数在[-1,
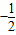 ]单调递减,在[
]单调递减,在[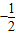 ,1]单调递增,
,1]单调递增,故当t=
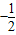 时,函数取最小值ymin=-4,
时,函数取最小值ymin=-4,当t=1时,函数取最大值ymax=5
故函数的值域为[-4,5]
故答案为:[-4,5]
点评:本题考查二次函数在闭区间的最值,利用二倍角的余弦公式化为关于t的二次函数的区间最值是解决问题的关键,属中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
将函数y=f(x)cosx的图象向左移
个单位后,再作关于x轴的对称变换得到的函数y=2cos2x-1的图象,则f(x)可以是( )
| π |
| 4 |
| A、-2cosx |
| B、2cosx |
| C、-2sinx |
| D、2sinx |
 函数y=2cos2x+sin2x的最小值是
函数y=2cos2x+sin2x的最小值是