题目内容
已知圆锥的母线长为2cm,底面直径为3cm,则过该圆锥两条母线的截面面积的最大值为
- A.4cm2
- B.
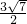 cm2
cm2 - C.2cm2
- D.
 cm2
cm2
D
分析:由圆锥的母线长为2cm,底面直径为3cm,知过该圆锥两条母线的截面是腰长为2,底边为3的等腰三角形,由此能求出截面面积的最大值.
解答:∵圆锥的母线长为2cm,底面直径为3cm,
∴过该圆锥两条母线的截面是腰长为2,底边为3的等腰三角形,
这个等腰三角形的高为 =
= ,
,
∴截面面积的最大值S= =
= .
.
故选D.
点评:本题考查圆锥的高,母线长,底面半径组成直角三角形这个知识点.解题时要认真审题,仔细解答.
分析:由圆锥的母线长为2cm,底面直径为3cm,知过该圆锥两条母线的截面是腰长为2,底边为3的等腰三角形,由此能求出截面面积的最大值.
解答:∵圆锥的母线长为2cm,底面直径为3cm,
∴过该圆锥两条母线的截面是腰长为2,底边为3的等腰三角形,
这个等腰三角形的高为
 =
= ,
,∴截面面积的最大值S=
 =
= .
.故选D.
点评:本题考查圆锥的高,母线长,底面半径组成直角三角形这个知识点.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 ,则该圆锥的侧面积是 .
,则该圆锥的侧面积是 . ,则该圆锥的侧面积是 .
,则该圆锥的侧面积是 . ,则该圆锥的侧面积是 .
,则该圆锥的侧面积是 .