题目内容
已知数列{an}满足a1=1,前n项和Sn=2an-n,(n∈N*)(1)证明:数列{an+1}是等比数列;
(2)试比较Sn与2-n的大小关系.
【答案】分析:(1)令n=1代入所给的式子求出a1+1的值,再由n≥2时,an=Sn-Sn,代入化简得到数列的递推公式,再求出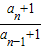 是常数,则结论得证;
是常数,则结论得证;
(2)根据(1)和等比数列的通项公式求出an,再代入Sn=2an-n化简,再作差:Sn-(2-n)并变形,由n的范围判断出符号,得到二者的大小关系.
解答:解:(1)当n=1时,a1=S1=2a1-1,
∴a1=1,解得a1+1=2,
当n≥2时,an=Sn-Sn=2an-2an-1-1,
∴an=2an-1+1,
∴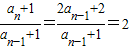
∴数列{an+1}是以2为首项以2为公比的等比数列.
(2)由(1)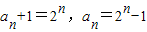 ,
,
∴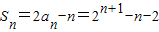
又∵n∈N*,n≥1,
∴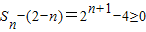
∴Sn≥2-n.
点评:本题考查了等比数列的证明,通项公式的应用,以及数列的项与前n项和之间的转化问题.
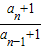 是常数,则结论得证;
是常数,则结论得证;(2)根据(1)和等比数列的通项公式求出an,再代入Sn=2an-n化简,再作差:Sn-(2-n)并变形,由n的范围判断出符号,得到二者的大小关系.
解答:解:(1)当n=1时,a1=S1=2a1-1,
∴a1=1,解得a1+1=2,
当n≥2时,an=Sn-Sn=2an-2an-1-1,
∴an=2an-1+1,
∴
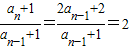
∴数列{an+1}是以2为首项以2为公比的等比数列.
(2)由(1)
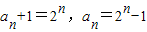 ,
,∴
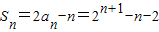
又∵n∈N*,n≥1,
∴
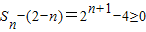
∴Sn≥2-n.
点评:本题考查了等比数列的证明,通项公式的应用,以及数列的项与前n项和之间的转化问题.

练习册系列答案
相关题目