题目内容

（2012•青岛一模）已知函数f(x)=xsin(x+
π
2
)，则f′(
π
2
)=（　　）
分析：求出原函数的导函数，在导函数中取x=
π
2
可得f′(
π
2
)的值．
解答：解：由f(x)=xsin(x+
π
2
)，得f′(x)=sin(x+
π
2
)+xcos(x+
π
2
)=cosx-xsinx．
所以f′(
π
2
)=cos
π
2
-
π
2
sin
π
2
=-
π
2
．
故选A．
点评：本题考查了导数的运算，解答的关键在于熟记基本初等函数的导数公式，是基础的运算题．
练习册系列答案
相关题目
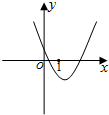（2012•青岛一模）已知a＞b，函数f（x）=（x-a）（x-b）的图象如图所示，则函数g（x）=loga（x+b）的图象可能为
（　　）
（2012•青岛一模）已知等差数列{an}的公差大于零，且a2，a4是方程x2-18x+65=0的两个根；各项均为正数的等比数列{bn}的前n项和为Sn，且满足b3=a3，S3=13．
（1）求数列{an}、{bn}的通项公式；
（2）若数列{cn}满足cn=
an ，n≤5
bn  ，n＞5
，求数列{cn}的前n项和Tn．
（2012•青岛一模）已知实数集R，集合M={x|0＜x＜2}，集合N={x|y=
1
x-1
}，则M∩（?RN）（　　）
（2012•青岛一模）已知锐角△ABC中内角A、B、C的对边分别为a、b、c，且a2+b2=c2+ab．
（Ⅰ）求角C的值；
（Ⅱ）设函数f（x）=sin（ωx-
π6
）-cosωx（ω＞0），且f（x）图象上相邻两最高点间的距离为π，求f（A）的取值范围．
（2012•青岛一模）已知点M在椭圆D：
x2
a2
+
y2
b2
=1（a＞b＞0）上，以M为圆心的圆与x轴相切于椭圆的右焦点，若圆M与y轴相交于A，B两点，且△ABM是边长为
2
6
3
的正三角形．
（Ⅰ）求椭圆D的方程；
（Ⅱ）设P是椭圆D上的一点，过点P的直线l交x轴于点F（-1，0），交y轴于点Q，若
QP
=2
PF
，求直线l的斜率；
（Ⅲ）过点G（0，-2）作直线GK与椭圆N：
3x2
a2
+
4y2
b2
=1左半部分交于H，K两点，又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R，S两点，试判断满足|GH|•|GK|=3|RF1|•|F1S|的直线GK是否存在？请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网