题目内容
(1)已知m>0,若10x=lg(10m)+lg  ;
;
(2)已知log1227=a,求log616的值.
解 (1)由10x=lg(10m)+lg  ,
,
可得10x=lg10=1,∴x=0.
(2)由log1227=a,得 =a,
=a,
∴lg 3= ,∴
,∴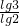 =
= .
.
∴log616= =
= =
= .
.
分析:(1)由10x=lg(10m)+lg ,利用对数的运算法则即可得出10x=lg 10=1,进而得出x.
,利用对数的运算法则即可得出10x=lg 10=1,进而得出x.
(2)由log1227=a,得 =a,可得
=a,可得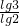 ,再利用对数的换底公式可得log616=
,再利用对数的换底公式可得log616= ,代入即可得出.
,代入即可得出.
点评:熟练掌握对数的运算法则和对数的换底公式是解题的关键.
 ,
,可得10x=lg10=1,∴x=0.
(2)由log1227=a,得
 =a,
=a,∴lg 3=
 ,∴
,∴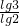 =
= .
.∴log616=
 =
= =
= .
.分析:(1)由10x=lg(10m)+lg
 ,利用对数的运算法则即可得出10x=lg 10=1,进而得出x.
,利用对数的运算法则即可得出10x=lg 10=1,进而得出x.(2)由log1227=a,得
 =a,可得
=a,可得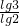 ,再利用对数的换底公式可得log616=
,再利用对数的换底公式可得log616= ,代入即可得出.
,代入即可得出.点评:熟练掌握对数的运算法则和对数的换底公式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目