题目内容
已知sinα+sinβ=
,求cosα+cosβ的最大值和最小值.
思路分析：令cosα+cosβ=x,然后利用函数思想.
解：令cosα+cosβ=x,
则得方程组：
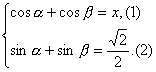
①2+②2得2+2cos(α-β)=x2+
，
∴cos(α-β)=
.
∵|cos(α-β)|≤1,
∴|
|≤1.
解之得:-
≤x≤
.
∴cosα+cosβ的最大值是
,最小值是-
.
练习册系列答案
相关题目
,求cosα+cosβ的最大值和最小值.题目内容
已知sinα+sinβ=,求cosα+cosβ的最大值和最小值.
思路分析：令cosα+cosβ=x,然后利用函数思想.
解：令cosα+cosβ=x,
则得方程组：
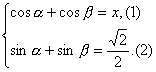
①2+②2得2+2cos(α-β)=x2+，
∴cos(α-β)=.
∵|cos(α-β)|≤1,
∴||≤1.
解之得:-≤x≤.
∴cosα+cosβ的最大值是,最小值是-.