题目内容
四边形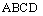 与
与 都是边长为
都是边长为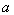 的正方形,点E是
的正方形,点E是 的中点,
的中点,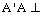 平面
平面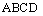
(1)求证: 平面
平面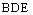 ;
;
(2)求证:平面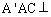 平面
平面 ;
;
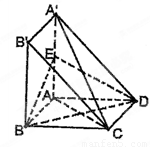
(3)求三棱锥A—BDE的体积
【答案】
(1)详见解析;(2)详见解析;(3)
【解析】
试题分析:(1)求证: 平面
平面 ,证明线面平行,先证明线线平行,即在平面
,证明线面平行,先证明线线平行,即在平面 找一条直线与
找一条直线与 平行,故设BD交AC于M,连结ME 由三角形的中位线定理可得
平行,故设BD交AC于M,连结ME 由三角形的中位线定理可得 ,结合线面平行的判定定理,即可得到
,结合线面平行的判定定理,即可得到 平面
平面 ;(2)求证:平面
;(2)求证:平面 平面
平面 ,先证明线面垂直,即证一个平面过另一个平面的垂线,根据已知条件,得到
,先证明线面垂直,即证一个平面过另一个平面的垂线,根据已知条件,得到 ,
, 由线面垂直的判定定理可得
由线面垂直的判定定理可得 平面
平面 ,再由面面垂直的判定定理,可得平面
,再由面面垂直的判定定理,可得平面 平面
平面 ;(3)求三棱锥
;(3)求三棱锥 的体积,直接求三棱锥
的体积,直接求三棱锥 的体积不好求,可进行等体积转化,即转化求三棱锥
的体积不好求,可进行等体积转化,即转化求三棱锥 的体积,而三棱锥
的体积,而三棱锥 的底面积及都能求出,从而得解
的底面积及都能求出,从而得解
试题解析:(1)设BD交AC于M,连结ME
∵ABCD为正方形,所以M为AC中点,
又∵E为 的中点 ∴ME为
的中点 ∴ME为 的中位线
的中位线
∴ 又∵
又∵ 平面
平面
 平面
平面
∴ 平面
平面 4分
4分
(2)∵ABCD为正方形 ∴
∵ 平面
平面 平面
平面
又 平面
平面 平面
平面 平面
平面
∵平面
 平面
平面
∴平面 平面
平面 8分
8分
(3) V=  12分
12分
考点:平面与平面垂直的判定;棱柱、棱锥、棱台的体积;直线与平面平行的判定

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 与
与 都是边长为
都是边长为 的正方形
的正方形 ,点E是
,点E是 的中点,
的中点,

 平面BDE;
平面BDE; ⊥平面BDE
⊥平面BDE 与
与 的比值。
的比值。 
 与
与 都是边长为
都是边长为 的正方形,点E是
的正方形,点E是 的中点,
的中点,

 ;
;  ;
; 与
与 的比值。
的比值。 与
与 都是边长为
都是边长为 的正方形,点E是
的正方形,点E是 的中点,
的中点, ⊥平面ABCD.
⊥平面ABCD. 

 平面BDE;
平面BDE; ⊥平面BDE.
⊥平面BDE. 与
与 都是边长为
都是边长为 的正方形,点E是
的正方形,点E是 的中点,
的中点,

 平面BDE;
平面BDE; ⊥平面BDE
⊥平面BDE 与
与 的比值。
的比值。 