题目内容
19.在菱形ABCD中,AB=2$\sqrt{3}$,∠B=$\frac{2π}{3}$,$\overrightarrow{BC}=2\overrightarrow{BE}$,$\overrightarrow{DA}=3\overrightarrow{DF}$,则$\overrightarrow{EF}•\overrightarrow{AC}$=-15.分析 如图所示,AB=2$\sqrt{3}$,D(-$\sqrt{3}$,0),B($\sqrt{3}$,0),A(0,-3),C(0,3),由于$\overrightarrow{BC}=2\overrightarrow{BE}$,$\overrightarrow{DA}=3\overrightarrow{DF}$,可得E$(\frac{\sqrt{3}}{2},-\frac{3}{2})$,F$(-\frac{2\sqrt{3}}{3},-2)$,利用坐标运算即可得出.
解答 解:如图所示,
AB=2$\sqrt{3}$,D(-$\sqrt{3}$,0),B($\sqrt{3}$,0),A(0,-3),C(0,3),
∵$\overrightarrow{BC}=2\overrightarrow{BE}$,$\overrightarrow{DA}=3\overrightarrow{DF}$,
∴E$(\frac{\sqrt{3}}{2},\frac{3}{2})$,F$(-\frac{2\sqrt{3}}{3},-1)$,$\overrightarrow{EF}$=$(-\frac{7\sqrt{3}}{6},-\frac{5}{2})$,
又$\overrightarrow{AC}$=(0,6),
∴$\overrightarrow{EF}•\overrightarrow{AC}$=-15.
故答案为:-15.
点评 本题考查了向量的数量积坐标运算性质、菱形的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.已知cos(π+x)=$\frac{4}{5}$,x∈(π,2π),则cos($\frac{π}{2}-x$)=( )
| A. | -$\frac{3}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
11.下列有关命题的说法正确的是( )
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R 均有x2+x+1<0” | |
| C. | 在△ABC中,“A>B”是“sinA>sinB”的充要条件 | |
| D. | “x≠2或y≠1”是“x+y≠3”既不充分也不必要条件 |
9.设等比数列{an}的公比q≠1,其前n项和为Sn,且${S_n}={q^n}+k$,则k=( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
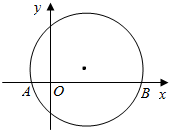 已知动圆M过点P(0,2),且在x轴上截得的弦AB的长为4.
已知动圆M过点P(0,2),且在x轴上截得的弦AB的长为4.