题目内容
已知点A（1，2）在椭圆
=1内，F的坐标为（2，0），在椭圆上求一点P使|PA|+2|PF|最小.
思路分析：用数形结合的方法探讨何时|PA|+2|PF|最小，进而确定P点.
解：∵a2=16,b2=12,?
∴c2=4,c=2.?
∴F为椭圆的右焦点，并且离心率为
=
.?
设P到右准线的距离为d，则
|PF|=
d,d=2|PF|.?
∴|PA|+2|PF|=|PA|+d.?
由几何性质可知，当P点的纵坐标（横坐标大于零）与A点的纵坐标相同时，|PA|+d最小.?
把y=2代入
=1得?
x=
，x=-
（舍去）,?
即点P（
，2）为所求.
温馨提示
由
得d=2|PF|是求P点的关键.
练习册系列答案
相关题目
选作题，本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
=1内，F的坐标为（2，0），在椭圆上求一点P使|PA|+2|PF|最小.
的属于特征值b的一个特征向量为
，求实数a、b的值．
（t为参数，p为正常数），求p的值．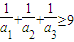
．