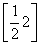题目内容
已知函数f(x)＝sin
.
(1)求f(x)的单调递增区间；
(2)若α是第二象限角，
，求cosα－sinα的值．
即sinα＋cosα＝
(cosα－sinα)2(sinα＋cosα)．
当sinα＋cosα＝0时，由α是第二象限角，知α＝
＋2kπ，k∈Z.此时，cosα－sinα＝－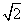
.
当sinα＋cosα≠0时，有(cosα－sinα)2＝
.
由α是第二象限角，知cosα－sinα<0，
此时cosα－sinα＝－
.
综上所述，cosα－sinα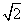＝－或－.
练习册系列答案
53随堂测系列答案
相关题目
＋x
等于( )
B.
D.
的长为l，弦AP的长为d，则函数d＝f(l)的图象大致为( )
＋sinα＝－
，则cos
等于( )
B．y＝cos
D．y＝cos
，函数y＝sinx＋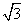
cosx的最大值为________，最小值为________．
(1)求实验室这一天的最大温差；
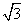，BC＝2，点E在线段CD上，若
，则μ的取值范围是( )
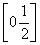D.