题目内容
已知函数f(x)=3x+2- -(3a+1)lnx (x>0,实数a为常数).
-(3a+1)lnx (x>0,实数a为常数).
(Ⅰ)a=4时 求函数f(x)在( ,+∞)上的最小值;
,+∞)上的最小值;
(Ⅱ)设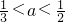 ,求证:不等式|f(x1)-f(x2)|<|x1-x2|对于任意不相等的x1,x2∈(
,求证:不等式|f(x1)-f(x2)|<|x1-x2|对于任意不相等的x1,x2∈( ,a)都成立.
,a)都成立.
(Ⅰ)解:a=4时,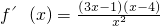 ,…(2分)
,…(2分)
令f′(x)<0,可得x∈(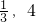 ),令f′(x)>0,由于x>
),令f′(x)>0,由于x> ,可得x∈(4,+∞),
,可得x∈(4,+∞),
∴f(x)在(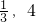 )上单调递减,在(4,+∞)上单调递增 …(4分)
)上单调递减,在(4,+∞)上单调递增 …(4分)
∴在区间( ,+∞)上,当x=4时,f(x)有最小值f(4)=13-26ln2 …(6分)
,+∞)上,当x=4时,f(x)有最小值f(4)=13-26ln2 …(6分)
(Ⅱ)证明:当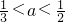 ,
,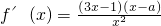 ,∴f(x)在(
,∴f(x)在( ,a)上单调递减,
,a)上单调递减,
不妨设x1<x2,则当x1,x2∈( ,a)时,f(x1)>f(x2),
,a)时,f(x1)>f(x2),
故不等式|f(x1)-f(x2)|<|x1-x2|等价于f(x1)+x1<f(x2)+x2,…(10分)
令函数g(x)=f(x)+x,则g′(x)=f′(x)+1=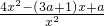
再令h(x)=4x2-(3a+1)x+a,对称轴x=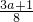 <
< (由于a<
(由于a< ),
),
∵h( )=
)= >0,h(a)=a2>0,∴h(x)>0当x∈(
>0,h(a)=a2>0,∴h(x)>0当x∈( ,a)时恒成立,
,a)时恒成立,
即g′(x)>0当x∈( ,a)时恒成立,所以g(x)在(
,a)时恒成立,所以g(x)在( ,a)上为增函数,
,a)上为增函数,
所以f(x1)+x1<f(x2)+x2,
从而不等式|f(x1)-f(x2)|<|x1-x2|对于任意不相等的x1,x2∈( ,a)都成立. …(15分)
,a)都成立. …(15分)
分析:(Ⅰ)求导函数,确定函数的单调性,即可求得函数的最值;
(Ⅱ)先确定f(x)在( ,a)上单调递减,不妨设x1<x2,则当x1,x2∈(
,a)上单调递减,不妨设x1<x2,则当x1,x2∈( ,a)时,f(x1)>f(x2),证明不等式|f(x1)-f(x2)|<|x1-x2|,即证f(x1)+x1<f(x2)+x2.
,a)时,f(x1)>f(x2),证明不等式|f(x1)-f(x2)|<|x1-x2|,即证f(x1)+x1<f(x2)+x2.
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.
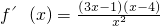 ,…(2分)
,…(2分)令f′(x)<0,可得x∈(
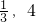 ),令f′(x)>0,由于x>
),令f′(x)>0,由于x> ,可得x∈(4,+∞),
,可得x∈(4,+∞),∴f(x)在(
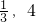 )上单调递减,在(4,+∞)上单调递增 …(4分)
)上单调递减,在(4,+∞)上单调递增 …(4分)∴在区间(
 ,+∞)上,当x=4时,f(x)有最小值f(4)=13-26ln2 …(6分)
,+∞)上,当x=4时,f(x)有最小值f(4)=13-26ln2 …(6分)(Ⅱ)证明:当
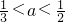 ,
,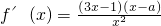 ,∴f(x)在(
,∴f(x)在( ,a)上单调递减,
,a)上单调递减,不妨设x1<x2,则当x1,x2∈(
 ,a)时,f(x1)>f(x2),
,a)时,f(x1)>f(x2),故不等式|f(x1)-f(x2)|<|x1-x2|等价于f(x1)+x1<f(x2)+x2,…(10分)
令函数g(x)=f(x)+x,则g′(x)=f′(x)+1=
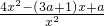
再令h(x)=4x2-(3a+1)x+a,对称轴x=
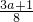 <
< (由于a<
(由于a< ),
),∵h(
 )=
)= >0,h(a)=a2>0,∴h(x)>0当x∈(
>0,h(a)=a2>0,∴h(x)>0当x∈( ,a)时恒成立,
,a)时恒成立,即g′(x)>0当x∈(
 ,a)时恒成立,所以g(x)在(
,a)时恒成立,所以g(x)在( ,a)上为增函数,
,a)上为增函数,所以f(x1)+x1<f(x2)+x2,
从而不等式|f(x1)-f(x2)|<|x1-x2|对于任意不相等的x1,x2∈(
 ,a)都成立. …(15分)
,a)都成立. …(15分)分析:(Ⅰ)求导函数,确定函数的单调性,即可求得函数的最值;
(Ⅱ)先确定f(x)在(
 ,a)上单调递减,不妨设x1<x2,则当x1,x2∈(
,a)上单调递减,不妨设x1<x2,则当x1,x2∈( ,a)时,f(x1)>f(x2),证明不等式|f(x1)-f(x2)|<|x1-x2|,即证f(x1)+x1<f(x2)+x2.
,a)时,f(x1)>f(x2),证明不等式|f(x1)-f(x2)|<|x1-x2|,即证f(x1)+x1<f(x2)+x2.点评:本题考查导数知识的运用,考查函数的单调性与最值,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=3•2x-1,则当x∈N时,数列{f(n+1)-f(n)}( )
| A、是等比数列 | B、是等差数列 | C、从第2项起是等比数列 | D、是常数列 |