题目内容
已知集合M={(x,y)|y=f(x)},若对于任意实数(x1,y2)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,则称集合M是“垂直对点集”,给出下列六个集合:
①M={(x,y)|y=-
}
②M={(x,y)|y=x2-1}
③M={(x,y)|y=ex-2}
④M={(x,y)|y=cosx}
⑤={(x,y)|y=2+sinx}
⑥M={(x,y)|y=lnx},
其中是“垂直对点集”的序号是 (写出所有是“垂直对点集”的序号).
①M={(x,y)|y=-
| 1 | x |
②M={(x,y)|y=x2-1}
③M={(x,y)|y=ex-2}
④M={(x,y)|y=cosx}
⑤={(x,y)|y=2+sinx}
⑥M={(x,y)|y=lnx},
其中是“垂直对点集”的序号是
分析:对于①,利用x1•x2+
=0无实数解,判断其正误即可.
对于③,画出函数y=ex-2图象,利用图象说明函数满足“垂直对点集”的定义,即可判断正误;
对于④,画出函数y=cosx图象,利用图象说明函数满足“垂直对点集”的定义,即可判断正误;
对于⑥,取一个特殊点(1,0)说明不满足“垂直对点集”定义.
| 1 |
| x1•x2 |
对于③,画出函数y=ex-2图象,利用图象说明函数满足“垂直对点集”的定义,即可判断正误;
对于④,画出函数y=cosx图象,利用图象说明函数满足“垂直对点集”的定义,即可判断正误;
对于⑥,取一个特殊点(1,0)说明不满足“垂直对点集”定义.
解答:解:对于①,注意到x1•x2+
∈(-∞,-2]∪[2,+∞),故x1•x2+
=0,即x1x2+y1y2=0无实数解,因此①不是“垂直对点集”;
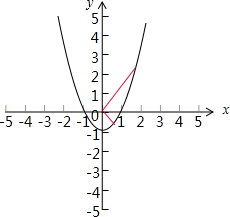
对于②,如下图,注意到过原点任意作一条直线与曲线y=x2-1相交,过原点与该直线垂直的直线必与曲线y=x2-1相交,因此②是“垂直对点集”;
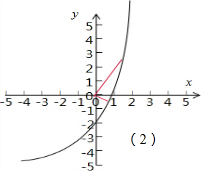
对于③,如下图,注意到过原点任意作一条直线与曲线y=ex-2相交,过原点与该直线垂直的直线必与曲线y=ex-2相交,因此③是“垂直对点集”;
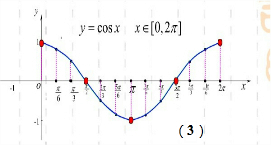
对于④,如下图,注意到过原点任意作一条直线与曲线y=cosx相交,过原点与该直线垂直的直线必与曲线y=cosx相交,因此④是“垂直对点集”;
对于⑤,注意到对于点(0,2)不存在(x2,y2)∈M,使得0×x2+2×2+sinx2=0,因为sinx2=-2与正弦函数的值域为[-1,1],因此⑤不是“垂直对点集”.
对于⑥,注意到对于点(1,0),不存在(x2,y2)∈M,使得1×x2+0×lnx2=0,因为x2=0与真数的限制条件x2>0矛盾,因此⑥不是“垂直对点集”.
故答案为:②③④
| 1 |
| x1•x2 |
| 1 |
| x1•x2 |
对于②,如下图,注意到过原点任意作一条直线与曲线y=x2-1相交,过原点与该直线垂直的直线必与曲线y=x2-1相交,因此②是“垂直对点集”;

对于③,如下图,注意到过原点任意作一条直线与曲线y=ex-2相交,过原点与该直线垂直的直线必与曲线y=ex-2相交,因此③是“垂直对点集”;

对于④,如下图,注意到过原点任意作一条直线与曲线y=cosx相交,过原点与该直线垂直的直线必与曲线y=cosx相交,因此④是“垂直对点集”;

对于⑤,注意到对于点(0,2)不存在(x2,y2)∈M,使得0×x2+2×2+sinx2=0,因为sinx2=-2与正弦函数的值域为[-1,1],因此⑤不是“垂直对点集”.
对于⑥,注意到对于点(1,0),不存在(x2,y2)∈M,使得1×x2+0×lnx2=0,因为x2=0与真数的限制条件x2>0矛盾,因此⑥不是“垂直对点集”.
故答案为:②③④
点评:点评:本题考查了命题真假的判断与应用,考查了元素与集合的关系,考查了数形结合的思想,解答的关键是对新定义的理解,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目