题目内容
已知椭圆 +
+ =1上的两点A、B与右焦点F2满足|AF2|+|BF2|=
=1上的两点A、B与右焦点F2满足|AF2|+|BF2|= a,又线段AB中点到左准线的距离为
a,又线段AB中点到左准线的距离为 ,求此椭圆方程.
,求此椭圆方程.
【答案】分析:可使用焦半径公式,设A(x1,y1),B(x2,y2),则|AF2|=a-ex1,|BF2|=a-ex2,从而可得 ,即AB中点横坐标,再由线段AB中点到左准线的距离为
,即AB中点横坐标,再由线段AB中点到左准线的距离为 ,列方程即可得a的值,最后确定椭圆方程
,列方程即可得a的值,最后确定椭圆方程
解答:解:设A(x1,y1),B(x2,y2),
∵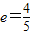 ,
,
由焦半径公式有a-ex1+a-ex2=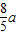 ,∴x1+x2=
,∴x1+x2= ,即AB中点横坐标为
,即AB中点横坐标为
又左准线方程为 ,∴
,∴ ,即a=1,
,即a=1,
∴椭圆方程为
点评:本题考查了椭圆的两个定义及椭圆的标准方程和几何性质,重点掌握两个定义及其应用.
 ,即AB中点横坐标,再由线段AB中点到左准线的距离为
,即AB中点横坐标,再由线段AB中点到左准线的距离为 ,列方程即可得a的值,最后确定椭圆方程
,列方程即可得a的值,最后确定椭圆方程解答:解:设A(x1,y1),B(x2,y2),
∵
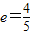 ,
,由焦半径公式有a-ex1+a-ex2=
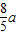 ,∴x1+x2=
,∴x1+x2= ,即AB中点横坐标为
,即AB中点横坐标为
又左准线方程为
 ,∴
,∴ ,即a=1,
,即a=1,∴椭圆方程为

点评:本题考查了椭圆的两个定义及椭圆的标准方程和几何性质,重点掌握两个定义及其应用.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 如图所示,F1,F2分别为椭圆C:
如图所示,F1,F2分别为椭圆C: 如图所示,F1、F2分别为椭圆C:
如图所示,F1、F2分别为椭圆C: 如图,椭圆
如图,椭圆 如图所示,F1、F2分别为椭圆C:
如图所示,F1、F2分别为椭圆C: