题目内容
若a是从-1,0,1,2四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求点P(a,b)在抛物线x2=y上的概率.
分析:用列举法求得点P(a,b)的全部情况共12种,而满足点P(a,b)在抛物线x2=y上的情况有3种,从而求得点P(a,b)在抛物线x2=y上的概率.
解答:解:点P(a,b)的全部情况有:(-1,0),(-1,1),(-1,2),(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)共12个,
设事件A“点P(a,b)在抛物线x2=y上”的基本事件有(-1,1),(1,1),(0,0),共3个,
故点P(a,b)在抛物线x2=y上的概率为
=
.
设事件A“点P(a,b)在抛物线x2=y上”的基本事件有(-1,1),(1,1),(0,0),共3个,
故点P(a,b)在抛物线x2=y上的概率为
| 3 |
| 12 |
| 1 |
| 4 |
点评:本题考主要查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,列举法,是解决古典概型问题的一种重要的解题方法,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
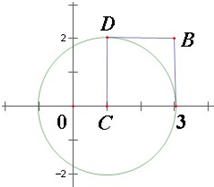 已知圆C:(x-1)2+y2=4,点(a,b).
已知圆C:(x-1)2+y2=4,点(a,b). (x>1),若a是从-1,0,1,2四数中任取一个,b是从1,2,3,4,5五数中任取一个,那么f(x)>b恒成立的概率为
(x>1),若a是从-1,0,1,2四数中任取一个,b是从1,2,3,4,5五数中任取一个,那么f(x)>b恒成立的概率为
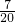


 (x>1),若a是从-1,0,1,2四数中任取一个,b是从1,2,3,4,5五数中任取一个,那么f(x)>b恒成立的概率为( )
(x>1),若a是从-1,0,1,2四数中任取一个,b是从1,2,3,4,5五数中任取一个,那么f(x)>b恒成立的概率为( )


