题目内容
已知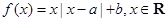 .
.
(Ⅰ)当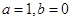 时,判断
时,判断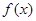 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(Ⅱ)当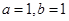 时,若
时,若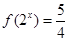 ,求
,求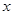 的值;
的值;
(Ⅲ)若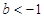 ,且对任何
,且对任何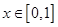 不等式
不等式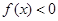 恒成立,求实数
恒成立,求实数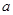 的取值范围.
的取值范围.
【答案】
(Ⅰ)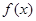 既不是奇函数,也不是偶函数;(Ⅱ)
既不是奇函数,也不是偶函数;(Ⅱ)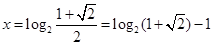 或
或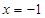 ;
;
(Ⅲ)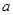 的取值范围是
的取值范围是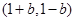 .
.
【解析】
试题分析:(Ⅰ)对函数奇偶性的判断,一定要结合函数特征先作大致判断,然后再根据奇函数偶函数的定义作严格的证明.当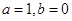 时,
时,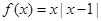 ,从解析式可以看出它既不是奇函数,也不是偶函数.对既不是奇函数,也不是偶函数的函数,一般取两个特殊值说明.
,从解析式可以看出它既不是奇函数,也不是偶函数.对既不是奇函数,也不是偶函数的函数,一般取两个特殊值说明.
(Ⅱ)当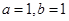 时,
时,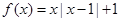 ,
由
,
由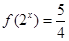 得
得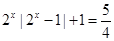 ,这是一个含有绝对值符号的不等式,对这种不等式,一般先分情况去绝对值符号.这又是一个含有指数式的不等式,对这种不等式,一般将指数式看作一个整体,先求出指数式的值,然后再利用指数式求出
,这是一个含有绝对值符号的不等式,对这种不等式,一般先分情况去绝对值符号.这又是一个含有指数式的不等式,对这种不等式,一般将指数式看作一个整体,先求出指数式的值,然后再利用指数式求出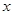 的值.
的值.
(Ⅲ)不等式恒成立的问题,一般有以下两种考虑,一是分离参数,二是直接求最值.在本题中,分离参数比较容易.分离参数时需要除以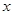 ,故首先考虑
,故首先考虑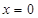 的情况. 易得
的情况. 易得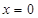 时,
时,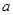 取任意实数,不等式
取任意实数,不等式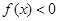 恒成立.
恒成立.
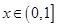 ,此时原不等式变为
,此时原不等式变为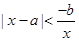 ;即
;即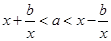 ,这时应满足:
,这时应满足: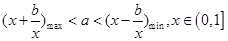 ,所以接下来就求
,所以接下来就求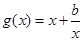 的最大值和
的最大值和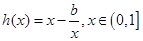 的最小值.
的最小值.
试题解析:(Ⅰ)当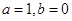 时,
时,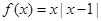 既不是奇函数也不是偶函数
既不是奇函数也不是偶函数
∵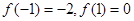 ,∴
,∴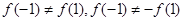
所以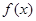 既不是奇函数,也不是偶函数 3分
既不是奇函数,也不是偶函数 3分
(Ⅱ)当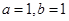 时,
时,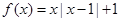 ,
由
,
由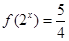 得
得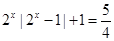
即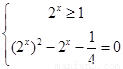 或
或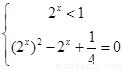
解得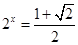 或
或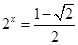 (舍),或
(舍),或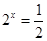 .
.
所以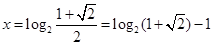 或
或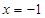 8分
8分
(Ⅲ)当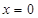 时,
时,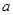 取任意实数,不等式
取任意实数,不等式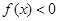 恒成立,
恒成立,
故只需考虑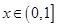 ,此时原不等式变为
,此时原不等式变为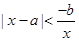
即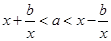
故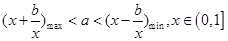
又函数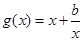 在
在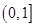 上单调递增,所以
上单调递增,所以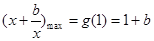 ;
;
对于函数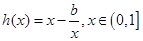
当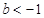 时,在
时,在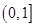 上
上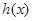 单调递减,
单调递减,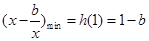 ,又
,又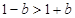 ,
,
所以,此时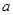 的取值范围是
的取值范围是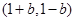 13分
13分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. 时,求函数
时,求函数 的定义域;
的定义域; 的不等式
的不等式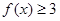 的解集是
的解集是 ,求
,求 的取值范围.
的取值范围.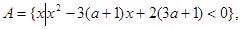
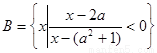 ,
, 时,求
时,求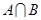 ;
; 的实数
的实数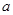 的取值范围。
的取值范围。 且
且 ,函数
,函数 ,当
,当 时,均有
时,均有 ,则实数
,则实数 的取值范围是
的取值范围是  B.
B.

 D.
D.
