题目内容
(2012•通州区一模)已知直线x-y+c=0与圆(x-1)2+y2=2有且只有一个公共点,那么c=
-3或1
-3或1
.分析:由直线与圆只有一个公共点,得到直线与圆相切,再由圆的方程找出圆心坐标和半径,利用点到直线的距离公式表示出圆心到直线的距离d,令d=r列出关于c的方程,求出方程的解即可得到c的值.
解答:解:由圆的方程(x-1)2+y2=2,得出圆心坐标为(1,0),半径r=
,
根据题意得:圆心到直线x-y+c=0的距离d=r,即
=
,
可得:1+c=2或1+c=-2,
解得:c=1或c=-3,
则c=-3或1.
故答案为:-3或1
| 2 |
根据题意得:圆心到直线x-y+c=0的距离d=r,即
| |1+c| | ||
|
| 2 |
可得:1+c=2或1+c=-2,
解得:c=1或c=-3,
则c=-3或1.
故答案为:-3或1
点评:此题考查了直线与圆的位置关系,直线与圆的位置关系由d与r的关系来确定(d表示圆心到直线的距离,r表示圆的半径),当d>r时,直线与圆相离;当d<r时,直线与圆相交;当d=r时,直线与圆相切.

练习册系列答案
相关题目
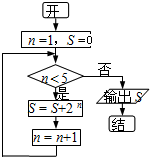 (2012•通州区一模)如图,程序框图所进行的求和运算是( )
(2012•通州区一模)如图,程序框图所进行的求和运算是( )