题目内容
 如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=2,AD=AE=EF=1,平面ABFE⊥平面ABCD.
如图,在多面体ABCDEF中,四边形ABCD是矩形,AB∥EF,∠EAB=90°,AB=2,AD=AE=EF=1,平面ABFE⊥平面ABCD.
(1)求直线FD与平面ABCD所成的角的正切值;
(2)求点D到平面BCF的距离;
(3)求二面角B-FC-D的大小.
解:(1)∵平面ABFE⊥平面ABCD,∠EAB=90°,
即EA⊥AB,而平面ABFE∩平面ABCD=AB,
∴EA⊥平面ABCD.作FH∥EA交AB于H,则FH⊥平面ABCD.
连接DH,则∠FDH为直线FD与平面ABCD所成的角.
在Rt△FHD中,∵FH=EA=1,DH= ,
,
∴
(2)∵平面ABFE⊥平面ABCD,EA⊥AB,
∴EA⊥平面ABCD.
分别以AD,AB,AE所在直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系,

则A(0,0,0)、D(1,0,0)、C(1,2,0)、E(0,0,1)、B(0,2,0)、
F(0,1,1),
∴ .
.
∵ ,∴
,∴ ⊥平面BCF,
⊥平面BCF,
即 =(0,1,1)为平面BCF的一个法向量,
=(0,1,1)为平面BCF的一个法向量,
又 ,
,
∴点D到平面BCF的距离为 .
.
(3)∵ ,设
,设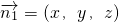 为平面CDEF的一个法向量,则
为平面CDEF的一个法向量,则 令x=1,得z=1,
令x=1,得z=1,
即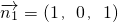 .
.
又(1)知, 为平面BCF的一个法向量,
为平面BCF的一个法向量,
∵< ,
, >=
>= ,
,
且二面角B-FC-D的平面角为钝角,
∴二面角B-FC-D的大小为120°.

分析:(1)根据面与面垂直的性质定理.得到线与面垂直,有面的垂线后面再做线与面的角,就好做了,得到线面角,在一个可解的三角形中,求出线面角的正切值.
(2)结合图形建立坐标系,写出要用的点的坐标,做出面的法向量,和要用的直线的对应的向量,根据点到直线的距离公式得到结果.
(3)在图形中的坐标系的基础上,写出要用的两个平面的法向量,求出法向量的坐标,其中有一个平面的法向量不用求出,是图形中存在的一个向量,求出两个平面所成的角.
点评:本题是一个立体几何的综合题目,考查的几个大的知识点,解题时要注意求线面角时注意用向量所求的是线面角的正弦值,不要出错.
即EA⊥AB,而平面ABFE∩平面ABCD=AB,
∴EA⊥平面ABCD.作FH∥EA交AB于H,则FH⊥平面ABCD.
连接DH,则∠FDH为直线FD与平面ABCD所成的角.
在Rt△FHD中,∵FH=EA=1,DH=
 ,
,∴

(2)∵平面ABFE⊥平面ABCD,EA⊥AB,
∴EA⊥平面ABCD.
分别以AD,AB,AE所在直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系,

则A(0,0,0)、D(1,0,0)、C(1,2,0)、E(0,0,1)、B(0,2,0)、
F(0,1,1),
∴
 .
.∵
 ,∴
,∴ ⊥平面BCF,
⊥平面BCF,即
 =(0,1,1)为平面BCF的一个法向量,
=(0,1,1)为平面BCF的一个法向量,又
 ,
,∴点D到平面BCF的距离为
 .
.(3)∵
 ,设
,设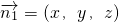 为平面CDEF的一个法向量,则
为平面CDEF的一个法向量,则 令x=1,得z=1,
令x=1,得z=1,即
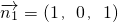 .
.又(1)知,
 为平面BCF的一个法向量,
为平面BCF的一个法向量,∵<
 ,
, >=
>= ,
,且二面角B-FC-D的平面角为钝角,
∴二面角B-FC-D的大小为120°.

分析:(1)根据面与面垂直的性质定理.得到线与面垂直,有面的垂线后面再做线与面的角,就好做了,得到线面角,在一个可解的三角形中,求出线面角的正切值.
(2)结合图形建立坐标系,写出要用的点的坐标,做出面的法向量,和要用的直线的对应的向量,根据点到直线的距离公式得到结果.
(3)在图形中的坐标系的基础上,写出要用的两个平面的法向量,求出法向量的坐标,其中有一个平面的法向量不用求出,是图形中存在的一个向量,求出两个平面所成的角.
点评:本题是一个立体几何的综合题目,考查的几个大的知识点,解题时要注意求线面角时注意用向量所求的是线面角的正弦值,不要出错.

练习册系列答案
相关题目
 如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1
如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC, (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC, (2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
(2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1= (2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
(2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=