题目内容
20. 在公比为2的等比数列{an}中,a2与a4的等差中项是5$\sqrt{3}$.
在公比为2的等比数列{an}中,a2与a4的等差中项是5$\sqrt{3}$.(Ⅰ)求a1的值;
(Ⅱ)若函数y=|a1|sin($\frac{π}{4}$x+φ),|φ|<π,的一部分图象如图所示,M(-1,|a1|),N(3,-|a1|)为图象上的两点,设∠MPN=β,其中P与坐标原点O重合,0<β<π,求tan(φ-β)的值.
分析 (Ⅰ)直接利用等比数列以及等差中项求出a1;
(Ⅱ)利用(Ⅰ)和函数的图象求出函数的解析式,通过余弦定理求出β的值,然后利用两角和与差的正切函数求出结果即可.
解答 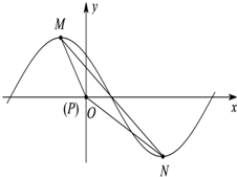 解:(Ⅰ)∵公比为2的等比数列{an}中,a2与a4的等差中项是5$\sqrt{3}$,
解:(Ⅰ)∵公比为2的等比数列{an}中,a2与a4的等差中项是5$\sqrt{3}$,
∴2a1+8a1=10$\sqrt{3}$,∴a1=$\sqrt{3}$;
(Ⅱ)函数y=$\sqrt{3}$sin($\frac{π}{4}$x+φ),|φ|<π的一部分图象如图所示,
M(-1,$\sqrt{3}$),N(3,-$\sqrt{3}$)为图象上的两点,
∴$\frac{π}{4}$×(-1)+φ=$\frac{π}{2}$,∴φ=$\frac{3π}{4}$.
∵点M、N在函数图象上,如图,连接MN,记∠MPN=β,
则在△MPN中,由余弦定理得
cosβ=$\frac{|PM{|}^{2}+|PN{|}^{2}-|MN{|}^{2}}{2|PM||PN|}$=$\frac{4+12-28}{8\sqrt{3}}$=-$\frac{\sqrt{3}}{2}$,
又∵0<β<π,∴β=$\frac{5}{6}π$,
∴φ-β=$\frac{3π}{4}$-$\frac{5}{6}π$=-$\frac{π}{12}$,
∴tan(φ-β)=-tan$\frac{π}{12}$=-tan($\frac{π}{4}$-$\frac{π}{6}$)=-2+$\sqrt{3}$.
点评 本题是一道数列与三角函数的综合题,涉及到等差中项的性质、两角和的正切公式、余弦定理等知识,属于中档题.

练习册系列答案
相关题目
3.函数f(x)=x3+3ax2+3[(a+2)x+1]有极大值又有极小值,则a的取值范围是( )
| A. | (-1,2) | B. | f(-2,1) | C. | (-∞,-1)∪(2,+∞) | D. | (-∞,-2)∪(1,+∞) |
 如图所示正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E,F且EF=$\sqrt{2}$,给出下列五个结论
如图所示正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E,F且EF=$\sqrt{2}$,给出下列五个结论 据统计某校学生在上学路上所需时间最多不超过120分钟,该校随机抽取部分新入校的学生就其上学路上所需时间(单位:分钟)进行调查,并将所得数据绘制成频率分布直方图.
据统计某校学生在上学路上所需时间最多不超过120分钟,该校随机抽取部分新入校的学生就其上学路上所需时间(单位:分钟)进行调查,并将所得数据绘制成频率分布直方图. 已知如图数阵,其中第n行含有n个元素,每一行元素都由连续正奇数组成,并且每一行元素中的最大数与后一行元素中的最小数是连续奇数.求数阵序列第n行中最大数an的表达式.
已知如图数阵,其中第n行含有n个元素,每一行元素都由连续正奇数组成,并且每一行元素中的最大数与后一行元素中的最小数是连续奇数.求数阵序列第n行中最大数an的表达式.