题目内容
已知向量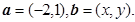
(1)若 分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足
分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足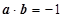 的概率.
的概率.
(2)若 在连续区间[1,6]上取值,求满足
在连续区间[1,6]上取值,求满足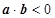 的概率.
的概率.
【答案】
(1)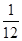 ;(2)
;(2)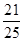 .
.
【解析】
试题分析:(1)掷一枚骰子的结果有6种,先后抛掷两次,所包含的基本事件总数为6×6=36个,由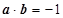 得
得 ,所以
,所以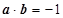 所包含的基本事件为
所包含的基本事件为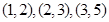 ,所求的概率为
,所求的概率为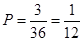 .
.
(2)若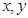 在连续区间[1,6]上取值,这符合几何概型的条件,事件的全部结果构成的区域
在连续区间[1,6]上取值,这符合几何概型的条件,事件的全部结果构成的区域
Ω={(x,y)|1≤x≤6,1≤y≤6},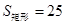 ,满足
,满足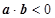 基本事件的结果为
基本事件的结果为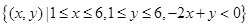 ,
,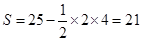 ,所求概率
,所求概率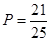 .
.
试题解析:(1)将一枚质地均匀的正方体骰子先后抛掷两次,所包含的基本事件总数为6×6=36个;由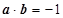 有-2x+y=-1,所以满足
有-2x+y=-1,所以满足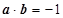 的基本事件为(1,1),(2,3),(3,5),共3个;故满足
的基本事件为(1,1),(2,3),(3,5),共3个;故满足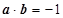 的概率为
的概率为 =
=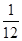 .
.
(2)若x,y在连续区间[1,6]上取值,则全部基本事件的结果为Ω={(x,y)|1≤x≤6,1≤y≤6};满足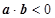 的基本事件的结果为A={(x,y)|1≤x≤6,1≤y≤6且-2x+y<0};画出图形如下图,
的基本事件的结果为A={(x,y)|1≤x≤6,1≤y≤6且-2x+y<0};画出图形如下图,
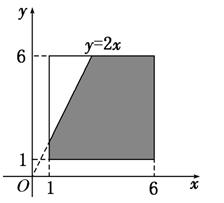
矩形的面积为S矩形=25,阴影部分的面积为S阴影=25-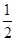 ×2×4=21,
×2×4=21,
故满足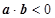 的概率为
的概率为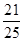 .
.
考点:1、古典概型的求法;2、几何概型的求法.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
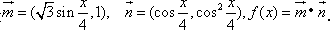

 求
求 的值;
的值; ,求
,求 的取值范围.
的取值范围.