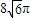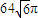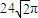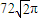Question

设A、B、C、D是球面上的四个点，且在同一平面内，AB=BC=CD=DA=3，球心到该平面的距离是球半径的一半，则球的体积是（　　）

• A、8

  6

  π
• B、64

  6

  π
• C、24

  2

  π
• D、72

  2

  π

Answer 1

分析：设出球的半径，球心到该平面的距离是球半径的一半，结合ABCD的对角线的一般，满足勾股定理，求出R即可求球的体积．

解答：解：设球的半径为R，由题意可得(

3 2

2

)2+(

R

2

)2=R2
R=

6

球的体积是：

4π

3

R3=8

6

π
故选A．

点评：本题考查球的体积，考查空间想象能力，计算能力，是基础题．