Question

如图，四棱锥P－ABCD中，底面ABCD是矩形，PA⊥底面ABCD，PA＝AB＝1，AD＝，点F是PB的中点，点E在边BC上移动．

(1)求三棱锥E－PAD的体积；

(2)点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；

(3)证明：无论点E在BC边的何处，都有PE⊥AF.

Answer 1

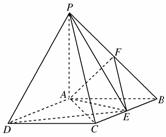
解：(1)∵PA⊥底面ABCD，∴PA⊥AD，

∴V_E－PAD＝S_△PAD·AB＝××1××1＝.

(2)当点E为BC的中点时，EF与平面PAC平行．

证明如下：∵在△PBC中，E、F分别为BC、PB的中点，

∴EF∥PC，又EF⊄平面PAC，

而PC⊂平面PAC，

∴EF∥平面PAC.

(3)证明：∵PA⊥平面ABCD，BE⊂平面ABCD，

∴BE⊥PA.又BE⊥AB，AB∩PA＝A，

∴BE⊥平面PAB，

又AF⊂平面PAB，∴AF⊥BE.

又PA＝AB＝1，点F是PB的中点，

∴AF⊥PB，又∵PB∩BE＝B，

∴AF⊥平面PBE.

∵PE⊂平面PBE，∴PE⊥AF.

故无论点E在BC边的何处，都有PE⊥AF.