题目内容
已知x∈R,且f(x+1)= -f(x),则f(x+2)=-f(x+1)=-[-f(x)]=f(x),得f(x)的一个周期为2,类比上述结论,请写出下列两个函数的一个周期:?
(1)已知a为正常数,x∈R,且f(x+a)=-f(x),则f(x)的一个周期为 ;?
(2)已知a为正常数,x∈R,且f(x+a)=![]() ,则f(x)的一个周期为 .?
,则f(x)的一个周期为 .?
2a;4a
解析:
(1)问,较容易猜出T=2a.第(2)问可以先建立三角模型:cot(x+![]() )=
)=![]() ,把cotx看作f(x)的一个原型,题中a相当于
,把cotx看作f(x)的一个原型,题中a相当于![]() ,由于f(x)=cotx的周期为T=π=4·
,由于f(x)=cotx的周期为T=π=4·![]() ,故可猜出4a为f(x)的一个周期,从而可转化求证f(x+4a)=f(x),验证方法:可先从f(x+2a)入手证得f(x+2a)=-
,故可猜出4a为f(x)的一个周期,从而可转化求证f(x+4a)=f(x),验证方法:可先从f(x+2a)入手证得f(x+2a)=-![]() ,所以f(x+4a)=f[(x+2a)+2a]=-
,所以f(x+4a)=f[(x+2a)+2a]=-![]() =f(x).
=f(x).

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
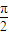 ,π),
,π), ,π),
,π),