题目内容
已知函数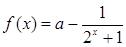 .
.
(1)如果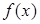 存在零点,求
存在零点,求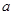 的取值范围
的取值范围
(2)是否存在常数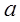 ,使
,使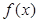 为奇函数?如果存在,求
为奇函数?如果存在,求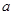 的值,如果不存在,说明理由。
的值,如果不存在,说明理由。
【答案】
(1) .(2)
.(2)
【解析】
试题分析:(1)函数的零点与方程的知识,通过极限的思维得到 的两边的范围,(2)由于定义为R,所以根据f(0)=0,解出
的两边的范围,(2)由于定义为R,所以根据f(0)=0,解出 的值,再把
的值,再把 代入用奇函数的定义论证.
代入用奇函数的定义论证.
试题解析:解:(1)令 得
得 ,
,
由于
欲使 有零点,
有零点,
(2) 易知函数 定义域为R.
定义域为R.
如果 为奇函数,则
为奇函数,则 ,可得
,可得
此时
∴ ,
,
所以,当 时
时 为奇函数.
为奇函数.
考点:1.函数的零点与方程根的关系.2.奇函数的概念.

练习册系列答案
相关题目

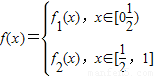 其中
其中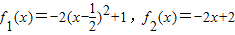
 的反函数为y=g(x),a1=1,a2=g(a1),…,
的反函数为y=g(x),a1=1,a2=g(a1),…,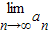 ;
;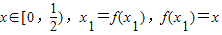 ,求x
,求x
 其中
其中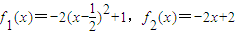
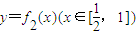 的反函数为y=g(x),a1=1,a2=g(a1),…,
的反函数为y=g(x),a1=1,a2=g(a1),…,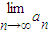 ;
; ,求x
,求x
 其中
其中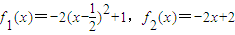
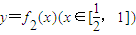 的反函数为y=g(x),a1=1,a2=g(a1),…,
的反函数为y=g(x),a1=1,a2=g(a1),…,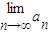 ;
;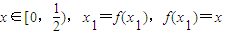 ,求x
,求x