Question

已知f（x）=x²-6x+5，则不等式组

f(x)+f(y)≤0 f(x)-f(y)≥0.

所表示的平面区域的面积为

4π

．

Answer 1

分析：由f（x）=x²-6x+5，知f（x）+f（y）=x²+y²-6x-6y≤0，f（x）-f（y）=（x-y）（x+y-6）≥0，所以不等式组

f(x)+f(y)≤0 f(x)-f(y)≥0.

所表示的平面区域是圆心为（3，3），半径为2

2

的圆的一半，由此能求出其面积．

解答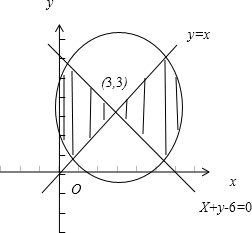：解：∵f（x）=x²-6x+5，
∴f（x）+f（y）=x²+y²-6x-6y≤0，
f（x）-f（y）=（x-y）（x+y-6）≥0，
∴不等式组

f(x)+f(y)≤0 f(x)-f(y)≥0.

所表示的平面区域是如图所求的阴影部分：
其面积是圆心为（3，3），半径为2

2

的圆的面积的一半，
即

1

2

×π×(2

2

)2=4π．
故答案为：4π．

点评：本题考查圆锥曲线的性质和应用，是中档题．解题时要认真审题，注意数形结合思想的重要应用．