题目内容
已知函数f(x)= 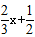 ,h(x)=
,h(x)=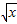 .
.
(Ⅰ)设函数F(x)=f(x)-h(x),求F(x)的单调区间与极值;
(Ⅱ)设a∈R,解关于x的方程㏒4[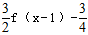 ]=㏒2h(a-x)-㏒2h(4-x);
]=㏒2h(a-x)-㏒2h(4-x);
(Ⅲ)试比较f(100)h(100)-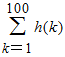 与
与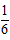 的大小.
的大小.
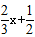 ,h(x)=
,h(x)=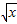 .
.(Ⅰ)设函数F(x)=f(x)-h(x),求F(x)的单调区间与极值;
(Ⅱ)设a∈R,解关于x的方程㏒4[
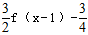 ]=㏒2h(a-x)-㏒2h(4-x);
]=㏒2h(a-x)-㏒2h(4-x);(Ⅲ)试比较f(100)h(100)-
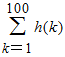 与
与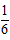 的大小.
的大小. (Ⅰ)由F(x)=f(x)-h(x)=
F'(x)=
当x∈(0,
故x∈(0,
故F(x)x∈(
F(x)在x=
(Ⅱ)原方程可化为log4(x-1)+log2 h(4-x)=log2h(a-x), 即
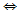
①当1<a≤4时,原方程有一解x=3-
②当4<a<5时,原方程有两解x=3±
③当a=5时,原方程有一解x=3; ④当a≤1或a>5时,原方程无解. (Ⅲ)设数列 {an}的前n项和为sn,且sn=f(n)g(n)-
从而有a1=s1=1. 当2<k≤100时,ak=sk-sk-1=
即对任意的2<k≤100,都有ak>
又因为a1=s1=1, 所以a1+a2+a3+…+a100>
故f(100)h(100)- 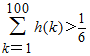 |

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|