题目内容
边长为1的等边三角形AOB,O为坐标原点,AB⊥x轴,以O为顶点且过A、B的抛物线方程是( )
(A)y2=![]() x (B)y2=-
x (B)y2=-![]() x
x
(C)y2=±![]() x (D) y2=±
x (D) y2=±![]() x
x
C.设AB⊥x轴于点D,则|OD|=1cos30°=![]() ,
,
|AD|=1sin30°=![]() ,所以A(
,所以A(![]() ,±
,±![]() )或A(-
)或A(-![]() ,±
,±![]() ).
).
由题意可设抛物线的方程为y2=2px.
将点A的坐标代入即可得2p=±![]() .故选C.
.故选C.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
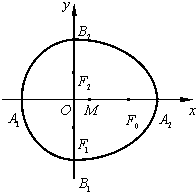 附加题:已知半椭圆
附加题:已知半椭圆 ,已知
,已知 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对 进行如下操作得到:将
进行如下操作得到:将 ).
).
 和
和 (
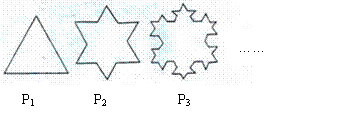
( ),求
),求 为曲线
为曲线 的递推关系式,并求
的递推关系式,并求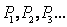 ,已知
,已知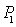 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对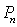 进行如下操作得到:将
进行如下操作得到:将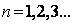 ).
).
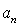 和
和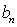 (
(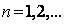 ),求
),求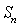 为曲线
为曲线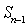 的递推关系式,并求
的递推关系式,并求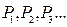 ,已知
,已知 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对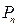 进行如下操作得到:将
进行如下操作得到:将 ).
).
 和
和 (
( ),求
),求 为曲线
为曲线 的递推关系式,并求
的递推关系式,并求