题目内容
已知集合A=
B
，试问是否存在实数a，使得A
B=
？
若存在，求出a的值；若不存在，请说明理由.
B，试问是否存在实数a，使得AB=？若存在，求出a的值；若不存在，请说明理由.
存在满足条件AB=的实数a,其取值范围是（-4，+∞）
B=的实数a,其取值范围是（-4，+∞） 方法一 假设存在实数a满足条件AB=，则有
（1）当A≠时，由AB
B=
，知集合A中的元素为非正数，
设方程x2+(2+a)x+1=0的两根为x1,x2,则由根与系数的关系，得
（2）当A=时，则有△=(2+a)2-4＜0，解得-4＜a＜0.
综上（1）、（2），知存在满足条件AB=的实数a,其取值范围是（-4，+∞）.
方法二 假设存在实数a满足条件AB≠，则方程x2+(2+a)x+1=0的两实数根x1,x2至少有一个为正，
因为x1·x2=1＞0，所以两根x1,x2均为正数.
则由根与系数的关系，得
解得
又∵集合
的补集为
∴存在满足条件AB=的实数a,其取值范围是（-4，+∞）.
B=，则有（1）当A≠
时，由ABB=，知集合A中的元素为非正数，设方程x2+(2+a)x+1=0的两根为x1,x2,则由根与系数的关系，得
（2）当A=
时，则有△=(2+a)2-4＜0，解得-4＜a＜0.综上（1）、（2），知存在满足条件A
B=的实数a,其取值范围是（-4，+∞）.方法二 假设存在实数a满足条件A
B≠，则方程x2+(2+a)x+1=0的两实数根x1,x2至少有一个为正，因为x1·x2=1＞0，所以两根x1,x2均为正数.
则由根与系数的关系，得
解得又∵集合
的补集为∴存在满足条件AB=的实数a,其取值范围是（-4，+∞）.
练习册系列答案
相关题目
,且A∪B=A,求由实数a组成的
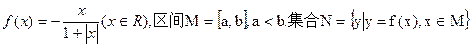，则使M=N成立的实数对(a,b)有（ ）
，
．
，
．
,
;
;
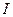为全集，
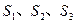是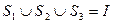
，则下面论断正确的是 （ ）
；
；
；
.
，
．
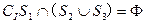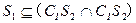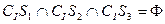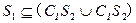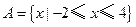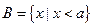，求实数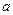
的取值范围；
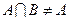，求实数