题目内容
如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B、C,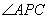 的平分线分别交AB、AC于点D、E.
的平分线分别交AB、AC于点D、E.
(1)证明: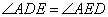 (2)若AC=AP,求
(2)若AC=AP,求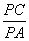 的值
的值

证明:(1)∵ PA是切线,AB是弦,∴ ∠BAP=∠C,又 ∵ ∠APD=∠CPE, ∴ ∠BAP+∠APD=∠C+∠CPE, ∵ ∠ADE=∠BAP+∠APD, ∠AED=∠C+∠CPE,∴ ∠ADE=∠AED.
(2)由(1)知∠BAP=∠C, 又∵ ∠APC=∠BPA,∴ △APC∽△BPA, ∴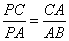 ,∵ AC=AP, ∴ ∠APC=∠C=∠BAP,由三角形内角和定理可知,∠APC+∠C+∠CAP=180°,∵ BC是圆O的直径,∴ ∠BAC=90°∴ ∠APC+∠C+∠BAP=180°-90°=90°,∴ ∠C=∠APC=∠BAP=
,∵ AC=AP, ∴ ∠APC=∠C=∠BAP,由三角形内角和定理可知,∠APC+∠C+∠CAP=180°,∵ BC是圆O的直径,∴ ∠BAC=90°∴ ∠APC+∠C+∠BAP=180°-90°=90°,∴ ∠C=∠APC=∠BAP=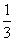 ×90°=30°.
×90°=30°.
在Rt△ABC中,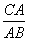 =
=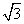 , ∴
, ∴ 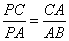 =
=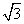

练习册系列答案
相关题目
 中,若
中,若 ,则
,则 的值为( )
的值为( ) B
B  C
C  D
D 
 中,
中, 为
为 与
与 的交点,若
的交点,若 ,则
,则 =
= 表示)
表示)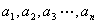 可得
可得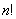 个不同的排列,每个排列为一行写成一个
个不同的排列,每个排列为一行写成一个 行
行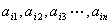 ,记
,记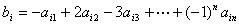 ,
,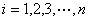 )例如由1、2、3排数阵知:由于此数阵中每一列各数之和都是12,所以
)例如由1、2、3排数阵知:由于此数阵中每一列各数之和都是12,所以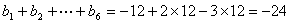 ,那么由1,2,3,4,5形成的数阵中,
,那么由1,2,3,4,5形成的数阵中,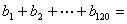 ( )
( ) 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, 的大小; (2)若
的大小; (2)若 ,求
,求 的取值范围.
的取值范围. 名学生负责校内
名学生负责校内 个不同地段的卫生工作,每个地段至少有
个不同地段的卫生工作,每个地段至少有 名学生的分配方案有( )
名学生的分配方案有( ) 种 B.
种 B. 种
种  种 D.
种 D. 种
种 中,若平面
中,若平面 上一动点
上一动点 到
到 和
和 的距离相等,则点
的距离相等,则点
 sin(
sin( -
- ),x∈R的最小正周期为( )
),x∈R的最小正周期为( ) B.π C.2π D.4π
B.π C.2π D.4π 的最小正周期为( )
的最小正周期为( ) B、
B、 C、
C、 D、
D、