Question

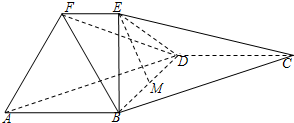（2012•朝阳区一模）在如图所示的几何体中，四边形ABCD为平行四边形，∠ABD=90°，EB⊥平面ABCD，EF∥AB，AB=2，EB=

3

，EF=1，BC=

13

，且M是BD的中点．
（Ⅰ）求证：EM∥平面ADF；
（Ⅱ）求二面角D-AF-B的大小；
（Ⅲ）在线段EB上是否存在一点P，使得CP与AF所成的角为30°？若存在，求出BP的长度；若不存在，请说明理由．

Answer 1

分析：（Ⅰ）证明EM∥平面ADF，利用线面平行的判定，证明EM平行于平面ADF中一条直线即可；也可建立如空间直角坐标系，求出平面ADF的一个法向量，证明

EM

⊥

n

；
（Ⅱ）平面ADF的一个法向量是

n

=(2，3，

3

)，

BD

=(3，0，0)是平面EBAF的一个法向量，利用向量的夹角公式，可求二面角D-AF-B的大小；
（Ⅲ）假设在线段EB上存在一点P，使得CP与AF所成的角为30°，不妨设P（0，0，t）（0≤t≤

3

），则

PC

=(3，-2，-t)，

AF

=(0，-1，

3

)，利用向量的夹角公式，求出t的值，即可得到结论．

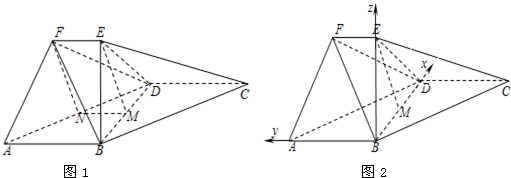
解答：（Ⅰ）证明：取AD的中点N，连接MN，NF．

在△DAB中，M是BD的中点，N是AD的中点，所以MN∥AB，MN=

1

2

AB，
又因为EF∥AB，EF=

1

2

AB，
所以MN∥EF且MN=EF．
所以四边形MNFE为平行四边形，
所以EM∥FN．
又因为FN?平面ADF，EM?平面ADF，
故EM∥平面ADF．…（4分）
解法二：因为EB⊥平面ABD，AB⊥BD，故以B为原点，建立如图2所示的空间直角坐标系B-xyz．…（1分）
由已知可得 B（0，0，0），A（0，2，0），D（3，0，0），C(3，-2，0)，E(0，0，

3

)，F(0，1，

3

)，M(

3

2

，0，0)
（Ⅰ）

EM

=(

3

2

，0，-

3

)，

AD

=(3，-2，0)，

AF

=(0，-1，

3

)．…（2分）
设平面ADF的一个法向量是

n

=（x，y，z）．
由

n • AD =0 n • AF =0

得

3x-2y=0 -y+ 3 z=0

令y=3，则

n

=(2，3，

3

)．…（3分）
又因为

EM

•

n

=(

3

2

，0，-

3

)•(2，3，

3

)=3+0-3=0，
所以

EM

⊥

n

，又EM?平面ADF，所以EM∥平面ADF．…（4分）
（Ⅱ）解：由（Ⅰ）可知平面ADF的一个法向量是

n

=(2，3，

3

)．
因为EB⊥平面ABD，所以EB⊥BD．
又因为AB⊥BD，所以BD⊥平面EBAF．
故

BD

=(3，0，0)是平面EBAF的一个法向量．
所以cos＜

BD

，

n

＞=

BD • n

| BD |•| n |

=

1

2

，又二面角D-AF-B为锐角，
故二面角D-AF-B的大小为60°．…（10分）
（Ⅲ）解：假设在线段EB上存在一点P，使得CP与AF所成的角为30°．
不妨设P（0，0，t）（0≤t≤

3

），则

PC

=(3，-2，-t)，

AF

=(0，-1，

3

)．
所以cos＜

PC

，

AF

＞=

| PC • AF |

| PC |•| AF |

=

|2- 3 t|

2 t2+13

，
由题意得|

2- 3 t

2 t2+13

|=

3

2

，化简得-4

3

t=35，
解得t=-

35

4 3

＜0．
所以在线段EB上不存在点P，使得CP与AF所成的角为30°．…（14分）

点评：本题考查线面平行，考查面面角，考查线面角，考查利用空间向量解决立体几何问题，确定平面的法向量，利用向量的夹角公式是关键