题目内容
已知直线l1：2x+3y-1=0与直线l2：6x+my+5=0相互垂直，则实数m的值为（ ）
分析：当m=0时，不满足条件；当m≠0时，利用两直线垂直斜率之积等于-1可得-
•（-
）=-1，解方程求得m值．
| 2 |
| 3 |
| 6 |
| m |
解答：解：当m=0 时，不满足条件．
当m≠0 时，-
•（-
）=-1，解得m=-4
故选：D
当m≠0 时，-
| 2 |
| 3 |
| 6 |
| m |
故选：D
点评：本题考查两直线垂直的性质，两直线垂直斜率之积等于-1，体现了分类讨论思想．
练习册系列答案
相关题目
已知直线l1：2x-my+1=0与l2：x+（m-1）y-1=0，则“m=2”是“l1⊥l2”的（ ）
| A、充分不必要条件 | B、必要不充分条件 | C、充分且必要条件 | D、既不充分又不必要条件 |
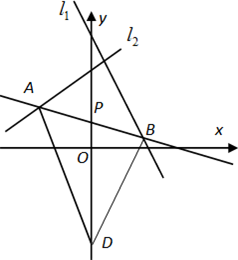如图，直线L过点P（0，1），夹在两已知直线l1：2x+y-8=0和l2：x-3y+10=0之间的线段AB恰被点P平分．