题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<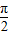 )的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x,0)和(x+2π,-2).
)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x,0)和(x+2π,-2).(1)求f(x)的解析式及x的值;
(2)求f(x)的增区间;
(3)若x∈[-π,π],求f(x)的值域.
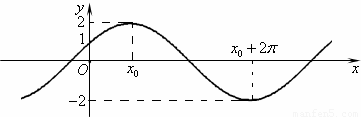
【答案】分析:(1)利用函数图象确定函数的振幅,周期,利用f(0)=1求出φ,求出f(x)的解析式,y轴右侧的第一个最高点即可求出x的值;
(2)通过正弦函数的单调增区间,直接求函数f(x)的增区间;
(3)通过x∈[-π,π],求出 x+
x+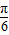 的范围,然后利用正弦函数的值域求f(x)的值域.
的范围,然后利用正弦函数的值域求f(x)的值域.
解答:解:由图象以及题意可知A=2,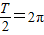 ,T=4π,ω=
,T=4π,ω=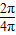 =
= ,
,
函数f(x)=2sin( x+φ),因为f(0)=1=2sinφ,|φ|<
x+φ),因为f(0)=1=2sinφ,|φ|<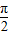 ,所以φ=
,所以φ=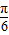 .
.
∴f(x)=2sin( x+
x+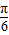 ).
).
由图象f(x)=2sin( x+
x+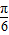 )=2,所以
)=2,所以 x+
x+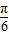 =
=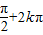 k∈Z,
k∈Z,
因为在y轴右侧的第一个最高点的坐标分别为(x,0),
所以x=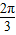 .
.
(2)由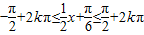 ,k∈Z,
,k∈Z,
得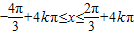 ,k∈Z,
,k∈Z,
所以函数的单调增区间为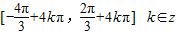 .
.
(3)∵x∈[-π,π],∴ x+
x+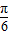
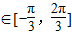 ,∴
,∴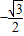 ≤sin(
≤sin( x+
x+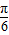 )≤1.
)≤1.
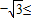 2sin(
2sin( x+
x+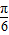 )≤2.
)≤2.
所以函数的值域为:[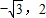 ].
].
点评:本题是中档题,考查函数解析式的求法,阿足协还是的单调增区间的求法,函数的值域的求法,考查计算能力.
(2)通过正弦函数的单调增区间,直接求函数f(x)的增区间;
(3)通过x∈[-π,π],求出
 x+
x+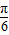 的范围,然后利用正弦函数的值域求f(x)的值域.
的范围,然后利用正弦函数的值域求f(x)的值域.解答:解:由图象以及题意可知A=2,
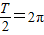 ,T=4π,ω=
,T=4π,ω=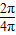 =
= ,
,函数f(x)=2sin(
 x+φ),因为f(0)=1=2sinφ,|φ|<
x+φ),因为f(0)=1=2sinφ,|φ|<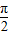 ,所以φ=
,所以φ=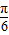 .
.∴f(x)=2sin(
 x+
x+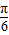 ).
).由图象f(x)=2sin(
 x+
x+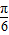 )=2,所以
)=2,所以 x+
x+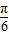 =
=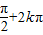 k∈Z,
k∈Z,因为在y轴右侧的第一个最高点的坐标分别为(x,0),
所以x=
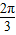 .
.(2)由
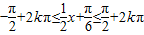 ,k∈Z,
,k∈Z,得
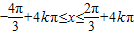 ,k∈Z,
,k∈Z,所以函数的单调增区间为
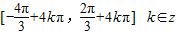 .
.(3)∵x∈[-π,π],∴
 x+
x+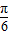
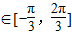 ,∴
,∴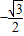 ≤sin(
≤sin( x+
x+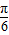 )≤1.
)≤1.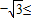 2sin(
2sin( x+
x+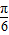 )≤2.
)≤2.所以函数的值域为:[
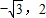 ].
].点评:本题是中档题,考查函数解析式的求法,阿足协还是的单调增区间的求法,函数的值域的求法,考查计算能力.

练习册系列答案
相关题目